Indholdsfortegnelse:

Video: QuickFFT: High Speed FFT til Arduino: 3 trin

2024 Forfatter: John Day | [email protected]. Sidst ændret: 2024-01-30 08:26

Typisk Arduino har begrænset RAM og processorkraft, og FFT er en beregningsintensiv proces. For mange realtidsapplikationer er det eneste krav at få frekvens med maksimal amplitude eller krævet for at detektere frekvensspidser.
I en af mine instruerbare udarbejdede jeg en kode til FFT, der kan findes herover: EasyFFT
Denne kode var i stand til at udføre FFT på op til 128 prøver på Arduino nano. Et højere prøvetal end dette er ikke muligt på grund af den begrænsede hukommelse af Arduino. Jeg har ændret funktionen lidt for at forbedre hastigheden og reducere hukommelsesforbruget. Denne ændring giver Arduino mulighed for at udføre FFT fem gange hurtigere og forbruger næsten halvdelen hukommelse. Denne instruktion dækker ikke Working of FFT, referencer til den kan findes på EasyFFT.
Trin 1: Arbejde




Den typiske FFT -funktion er ændret for at forbedre hastigheden med mindre nøjagtighed. Som vist på billedet skal et testsignal multipliceres med sinus- eller cosinusbølgeformer. Disse værdier kan være mellem 0 til 1, så det er et must at lave flydende multiplikation. i Arduino er flydende multiplikation langsom sammenlignet med heltalsoperationer.
I denne funktion erstattes sinus/cosinusbølgen med en firkantbølge. Da vi skal multiplicere et testsignal med en firkantbølge, der kan have værdi 0, 1 eller -1. På grund af det kan vi erstatte flydende multiplikation til ganske enkelt heltal addition eller subtraktion. For Arduino er heltal addition eller subtraktion omkring 5 gange hurtigere. Dette gør løsningen omkring 5 gange hurtigere.
På grund af denne ændring kan nu frekvensbakkeværdier gemmes som et heltal (som tidligere var flydende), og vi får en anden fordel ved lavere hukommelsesforbrug. I Arduino Nano forbruger int 2 byte hukommelse, mens float forbruger 4 byte hukommelse. På grund af denne fordel i den nye kode er vi i stand til at udføre FFT for næsten 256 prøver (tidligere 128 prøver).
I Normal FFT havde vi brug for at gemme sinusværdien for at gøre en løsning hurtigere. I ny funktion, da vi ikke længere krævede sinus/cosinus -værdier, kan vi eliminere det og spare noget hukommelse.
Gennemførelse:
Implementering af denne funktion er ligetil. Vi kan simpelthen kopiere funktionen ved kodens ens. Denne funktion kan udføres ved hjælp af nedenstående kommando:
float f = Q_FFT (data, 256, 100); I funktion Q_FFT, data: dette udtryk er en matrix med signalværdier, den anbefalede stikprøvestørrelse er 2, 4, 8, 32, 64, 128, 256, 512, … og fremefter. hvis prøvestørrelsen ikke tilhører disse værdier, klippes den til den nærmeste underside af værdier. for eksempel, hvis prøvestørrelsen er 75, udføres FFT for 64 antal prøver. Maks. Antal prøvestørrelser er begrænset af tilgængelig RAM på Arduino.
Det andet udtryk angiver antallet af prøver i et array, og det sidste udtryk er samplingsfrekvens i Hz.
Trin 2: Kode
Dette afsnit forklarer den ændring, der er foretaget i EasyFFT -kode, der skal tages i betragtning, mens der foretages ændringer i koden, 1. Som forklaret før bruges her heltal til at lave FFT. Int in Arduino er et 16 -bit tal og kan indeholde værdier fra -32768 til 32768. Når værdien af denne int overstiger dette område, forårsager det problemet. at fjerne dette problem efter nogensinde niveaueregning. hvis nogen af værdierne overstiger 15000 komplette arrays vil blive divideret med 100. dette forhindrer inten i at flyde over.
2. Amplitudeberegning: For at beregne amplitude skal den reelle og imaginære del kvadreres, og kvadratroden af summen er påkrævet. kvadrering og kvadratroden af funktionen tager tid. For at gøre processen hurtigere vil denne kode simpelthen gøre nogle af størrelserne på virkelige og imaginære dele. Dette er helt sikkert mindre præcist og kan i nogle tilfælde føre til den forkerte konklusion. du kan vælge at vende tilbage til den normale metode til størrelsesberegning, men det vil tage mere tid, og du skal også lave et arrangement for at gemme disse tal.
3. Denne kode har ikke et modul til detektering af flere spidser. Det vælger simpelthen værdien med maksimal amplitude (undtagen det første tal, der er DC -offset). Hvis du har brug for flere toppe, kan du henvise til EasyFFT -kode og foretage den nødvendige ændring her. I så fald skal en række array/variabler også erklæres som en global variabel.
4. Funktionen indeholder følgende linje:
usigneret int Pow2 [13] = {1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048};
erklærer de ovennævnte variabler som en global variabel (indsætter den i starten af koden) vil spare et sted 1 millisekunder tid ved hver udførelse.
5. I modsætning til EasyFFT -funktionen, hvor de 5 bedste toppe blev gemt i det foruddefinerede array. Denne funktion returnerer en float -værdi. denne værdi repræsenterer frekvensen med maksimal amplitude i Hz. Så repræsentationen af kode vil se sådan ud.
float f = Q_FFT (data, 256, 100);
6. Peak Detection: Når frekvens med maksimal amplitude er fundet, bruger denne funktion en amplitude af frekvens lige før og efter den til at beregne de nøjagtige resultater. Amplitude brugt i denne beregning er også summen af modul (ikke kvadratroden af summen af kvadrater)
hvis Fn er frekvensen med maksimal amplitude, kan frekvensen beregnes ud fra nedenstående formel.
Faktisk F = (A n-1 *Fn-1+An-1 *Fn-1+An-1 *Fn-1) / (An-1+An+An+1)
hvor An er amplitude af n frekvensen og Fn-1 er frekvensværdi.
Trin 3: Resultater:


Løsningstid er vist i ovenstående billedsammenligning med EasyFFT. Hastighed vist med sammenligningen.
For eksempeldata med 3 sinusformede bølger med forskellige frekvenser vises. Resultatet fra QuickFFT sammenlignes med Scilab -output. Som vi kan se på billedet matcher 3 toppe med maksimal amplitude med Scilab -output. Outputtet består imidlertid af masser af støj, hvilket kan være vildledende for nogle applikationer. Så det tilrådes at kontrollere koden korrekt, inden du ansøger om din ansøgning.
Jeg håber, at du fandt denne kode nyttig til dit projekt. Hvis du har spørgsmål eller forslag, bedes du kommentere.
Anbefalede:
Stepper Speed Control Menu drevet til Arduino: 6 trin

Stepper Speed Control Menu Drevet til Arduino: Dette SpeedStepper -bibliotek er en omskrivning af AccelStepper -biblioteket for at tillade hastighedskontrol af trinmotoren. SpeedStepper -biblioteket lader dig ændre den indstillede motorhastighed og derefter accelerere/bremse til den nye indstillede hastighed ved hjælp af den samme algorit
EasyFFT: Fast Fourier Transform (FFT) til Arduino: 6 trin

EasyFFT: Fast Fourier Transform (FFT) til Arduino: Måling af frekvens fra det indfangede signal kan være en vanskelig opgave, især på Arduino, da den har lavere beregningseffekt. Der er metoder til rådighed til at fange nulkryds, hvor frekvensen registreres ved at kontrollere, hvor mange gange
Sådan programmeres IR-dekoder til multi-speed vekselstrømsmotorstyring: 7 trin
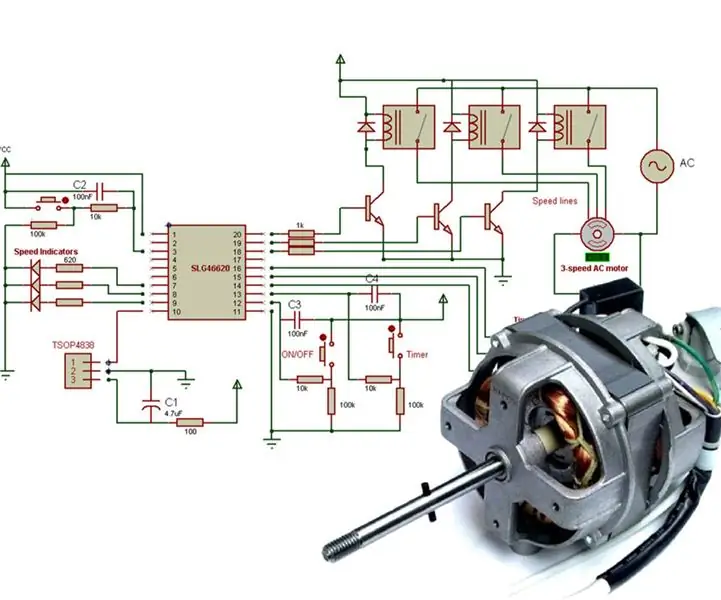
Sådan programmeres IR-dekoder til multi-speed vekselstrømsmotorstyring: Enfasede vekselstrømsmotorer findes typisk i husholdningsartikler som f.eks. Ventilatorer, og deres hastighed kan let kontrolleres, når der bruges et antal diskrete viklinger til indstillede hastigheder. I denne Instructable bygger vi en digital controller, som en
High Speed Gaming Laptop: 9 trin (med billeder)

High Speed Gaming Laptop: HiFriends, I dag vil jeg vise dig, hvordan du laver den mest kraftfulde og hurtige laptop i lommestørrelse med indbygget Windows 10-operativsystem derhjemme. I denne artikel vil jeg give dig alle oplysninger, så du nemt kan bygge dette hjemme
High Speed Flash -fotografering: 6 trin (med billeder)

High Speed Flash Photography: Dette er et billede af en skruetrækker midt i studsen. Efter at have læst om højhastighedsfotografering i et magasin blev jeg inspireret til at grave igennem mit skab og se, hvad jeg kunne finde på. Jeg brugte en hjemmelavet make-screen til at udløse blitzen, mens min digitale
