CNC Tromleplotter: 13 trin (med billeder)

2024 Forfatter: John Day | [email protected]. Sidst ændret: 2024-01-30 08:28

Denne instruktør beskriver en A4/A3 plotter fremstillet af en sektion af plastrør, to BYJ-48 stepper motorer og en SG-90 servo. I det væsentlige er det en plotter med flad seng rullet op i en tromle.

Den ene motor roterer tromlen, mens den anden flytter printhovedet. Servoen bruges til at hæve og sænke pennen.

Denne plotter har en række fordele i forhold til en traditionel flatbed plotter:

• betydeligt mindre fodaftryk
• kræver kun en lineær styreskinne
• enkel at konstruere
• billig

En indbygget tolk accepterer gcode-output fra Inkscape.

Kommunikation med plotteren sker via et bluetooth -link.

Plotteren er kompatibel med CNC Graphics Tablet beskrevet i min instruerbare

Selvom det ikke er et præcisionsinstrument, er denne plotters nøjagtighed tilfredsstillende med det tilsigtede formål at overføre akvarelkonturer til papir.

Trin 1: Kredsløbet

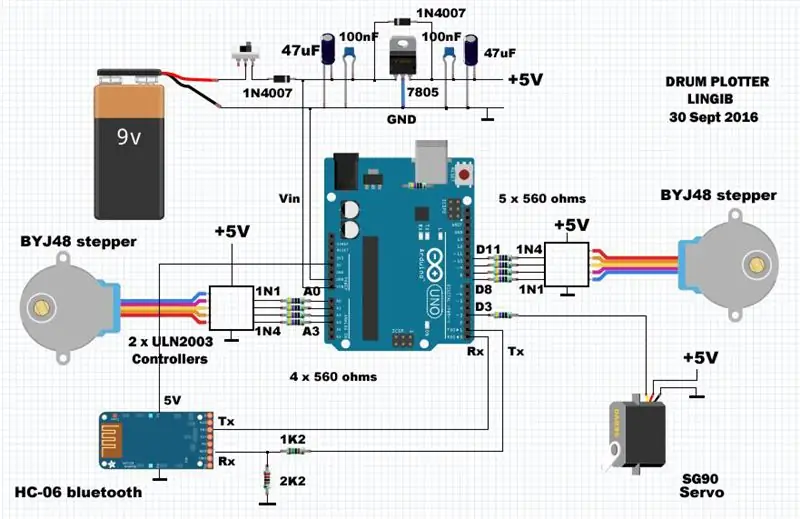
Kredsløbet består af en Arduino UNO R3 mikrokontroller og et brugerdefineret skjold, hvor de diskrete komponenter er monteret. Strøm tilføres via en ekstern 5 volt 1 amp regulator. Den gennemsnitlige strøm er omkring 500mA.

BYJ-48-trinmotorer er fastgjort til PORTB (ben D8, D9, D10, D11) og PORTC (ben A0, A1, A2, A3). SG-90 pen-lift servo er fastgjort til pin D3.

De 560 ohm modstande, som kan udelades, giver arduinoen et mål for kortslutningsbeskyttelse, hvis noget skulle gå galt. De gør det også lettere at tilslutte skjoldet, da de fungerer som "springere" hen over forsyningsskinnerne.

Modstanderne 1k2 og 2K2 forhindrer beskadigelse af HC-06 bluetooth-modulet [1] ved at tabe 5 volt udgangen fra arduinoen til 3,3 volt.

[1] Tag HC-06 bluetooth-modulet ud, når du uploader kode til arduinoen via USB-porten. Dette vil undgå eventuelle serielle portkonflikter.

Trin 2: Det lineære drev

Det lineære drev er lavet af en længde på 3 mm x 32 mm aluminiumstang, en strimmel af aluminiumsplade og fire små kuglelejeremskiver.

Aluminium fås fra de fleste isenkræmmere. U624ZZ 4x13x7mm U-rille remskiver er tilgængelige fra

Enkelt håndværktøj er alt, hvad du har brug for. Skær aluminiumstangen, så den passer til dine plottermål.

Motorenheden

Monter BJY-48-trinmotoren gennem stangen i den ene ende, og fastgør en GT2 20 tand, 5 mm boring, remskive til motorakslen. Monter nu en anden GT2 remskive i den anden ende af din stang, så remskiven kan rotere frit. Jeg brugte en 5 mm diameter rørformet (radio) afstandsstykke og en 3 mm bolt for at opnå dette.

Sløjf nu en længde af GT2 tandrem rundt om remskiverne. Tilslut tandremsslutterne ved hjælp af et halvt twist, så tænderne fletter sig sammen og fastgøres med et kabelbinder.

Til sidst fastgøres vognen til tandremmen med et kabelbinder.

Vognenheden

Vognenheden er fremstillet af en strimmel aluminiumsplade [1], som U624ZZ remskiver er boltet på. Brug om nødvendigt en 4 mm skive til at fjerne remskiverne fra aluminiumspladen.

Remskiverne, der har en 4 mm rille, ligger over aluminiumstangen øverst og nederst, så der ikke er nogen lodret bevægelse, men aluminiumsstrimlen bevæger sig frit til venstre og højre.

For at sikre, at vognen kører frit, skal du først montere de to øverste remskiver og derefter markere placeringen af de to nederste remskiver med remskiverne på stangen. Hullerne til disse to remskiver kan nu bores. Brug først en lille "pilot" boremaskine for at forhindre den større 4 mm boremaskine i at køre.

Inden du bøjer aluminiumstrimlen til et "U", skal du bore et hul øverst og nederst, så det passer til din pennediameter. Afslut nu svingene.

Fastgør tandremmen til vognen ved hjælp af et kabelbinder og en 3 mm bolt mellem de to øverste remskiver.

Pen-lift-samlingen

Fastgør en SG-90-servo til toppen af vognenheden ved hjælp af et eller to kabelbindere.

Slip din pen ned i de to huller, du har boret. Sørg for, at pennen glider frit op og ned.

Fastgør en "krave" til din pen, så pennen er lige uden for tromlen, når servoen er i pen-op-position.

[1] Aluminium kan skæres ved at skære begge sider af arket med en skarp kniv (kassefræser) og derefter bøje snittet ud over kanten af et bord. Et par vrikker og arket vil knække og efterlade en lige pause. I modsætning til tin-snips knækker denne metode ikke aluminiumet.

Trin 3: Tromlen

Tromlen omfatter en sektion af plastrør med to træpropper [1].

Brug et kompas, der er indstillet til den indvendige radius af dit rør, til at tegne konturerne på slutstikket. Skær nu rundt om hver kontur ved hjælp af en fin klingsav ("coping", "fret"), og tilpass derefter hver endeprop ved hjælp af en trærasp. Fastgør endepropperne ved hjælp af små skruer, der er forsænket.

En 6 mm konstruktionsbolt gennem midten af hver endeprop danner akslen.

Tromlemål

Tromledimensionerne bestemmes af din papirstørrelse. En tromlediameter på 100 mm understøtter A4 portræt og A3 liggende. En tromlediameter på 80 mm understøtter kun A4 -liggende. Brug så lille en tromlediameter som muligt for at reducere inertien … BYJ-48-motorerne er kun små.

En tromlediameter på 90 mm er ideel til A4 -portræt og A3 liggende papir, da de modsatte kanter, når de vikles rundt om tromlen, overlapper med cirka 10 mm, hvilket betyder, at du kun har en søm til at tape på plads.

Drejning af tromlen

Hver aksel passerer gennem en aluminiumsbeslag, så tromlen kan rotere frit. Endeflåd forhindres ved hjælp af en GT-2, 20 tand, 6 mm boring, remskive fastgjort til akslen i den ene ende. Et kontinuerligt GT-2 tandrem forbinder BJY-48-gearmotoren med tromlen. Motoren kræver en remskive med en borestørrelse på 5 mm.

[1] Plastikpropper er tilgængelige til de fleste rørdiametre, men blev afvist, da de passede over røret frem for indvendigt, og plasten har en tendens til at bøje. De ville nok være i orden, hvis der blev brugt en kontinuerlig aksel i stedet for boltene … men så kræver du en metode til at fastgøre akslen til endepropperne.

Trin 4: Konstruktionstip

Sørg for, at pennen bevæger sig langs midten af tromlen. Dette kan opnås ved at skære hjørnerne ud af træstøtterne. Hvis pennen er i midten, vil den have en tendens til at glide ned langs siden af tromlen.

Nøjagtig boring af de to penhuller er vigtig. Enhver vingling i pennestyret eller vognenheden vil forårsage vingler langs X-aksen.

Spænd ikke GT-2-tandremmen for meget … de skal bare være stramme. BYJ-48-trinmotorer har ikke meget moment.

BJY-48-trinmotorer udviser ofte små mængder tilbageslag, der er ubetydelig langs X-aksen, men er bekymret, når det kommer til Y-aksen. Årsagen til dette er, at en rotation af Y-aksemotoren svarer til en rotation af tromlen, hvorimod penvognen kræver mange omdrejninger af X-aksemotoren for at krydse tromlens længde. Enhver Y-akse modreaktion kan elimineres ved at holde et konstant drejningsmoment på tromlen. En enkel metode er at fastgøre en lille vægt til en nylonsnor, der er viklet rundt om tromlen.

Trin 5: Bresenhams stregtegningsalgoritme

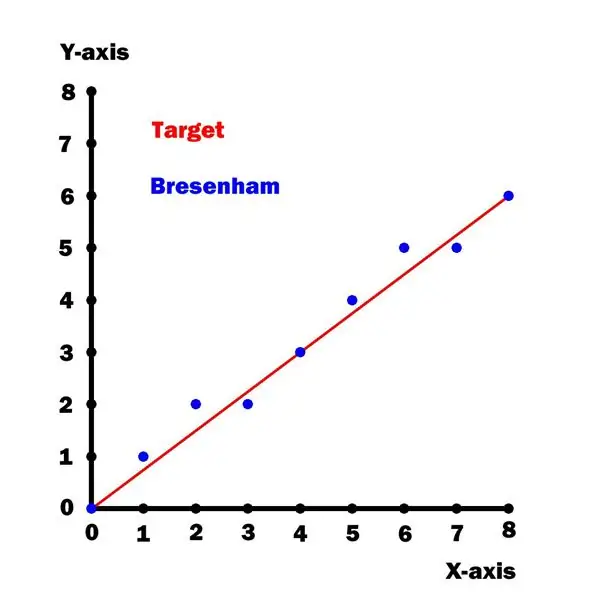
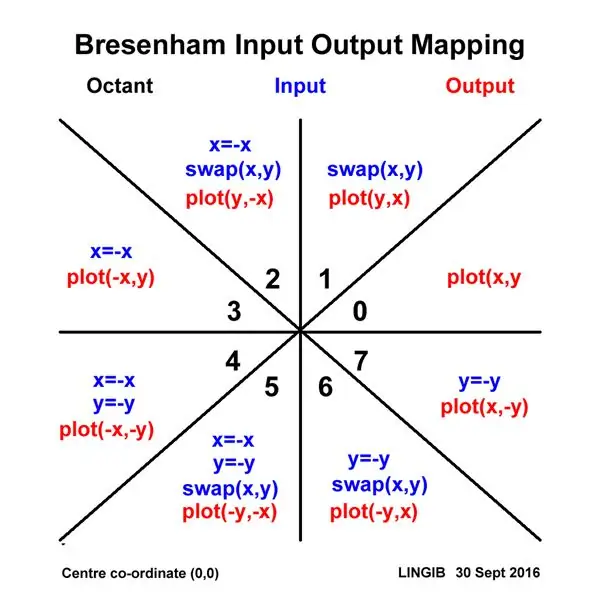
Denne plotter bruger en optimeret version [1] af Bresenhams stregtegningsalgoritme. Desværre er denne algoritme kun gyldig for liniehældninger mindre end eller lig med 45 grader (dvs. en oktant af en cirkel).

For at komme uden om denne begrænsning "kortlægger" jeg alle XY -input til den første "oktant", og derefter "fjerner kort" dem, når det er tid til at plotte. Input- og outputmappefunktionerne for at opnå dette er vist i diagrammet ovenfor.

Afledning

Resten af dette trin kan udelades, hvis du kender Bresenhams algoritme.

Lad os tegne en linje fra (0, 0) til (x1, y1), hvor:

• x1 = 8 = vandret afstand
• y1 = 6 = lodret afstand

Ligningen for en lige linje, der passerer gennem oprindelsen (0, 0) er givet ved ligningen y = m*x, hvor:

m = y1/x1 = 6/8 = 0,75 = hældning

Enkel algoritme

En simpel algoritme til at plotte denne linje er:

• int x1 = 8;
• int y1 = 6;
• flyde m = y1/x1;
• plot (0, 0);
• for (int x = 1; x <= x1; x ++) {
• int y = rund (m*x);
• plot (x, y);
• }

Tabel 1: Enkel algoritme

x	m	m*x	y
0	0.75	0	0
1	0.75	0.75	1
2	0.75	1.5	2
3	0.75	2.25	2
4	0.75	3	3
5	0.75	3.75	4
6	0.75	4.5	5
7	0.75	5.25	5
8	0.75	6	6

Der er to problemer med denne simple algoritme:

• hovedsløjfen indeholder en multiplikation, som er langsom
• den bruger flydende tal, hvilket også er langsomt

En graf over y mod x for denne linje er vist ovenfor.

Bresenhams algoritme

Bresenham introducerede begrebet et fejlbegreb 'e', der initialiseres til nul. Han indså, at m*x -værdierne vist i tabel 1 kan opnås ved successiv tilføjelse af 'm' til 'e'. Han indså endvidere, at y kun øges, hvis brøkdelen af m*x er større end 0,5. For at holde sin sammenligning inden for området 0 <= 0,5 <= 1 trækker han 1 fra 'e', når y øges.

• int x1 = 8;
• int y1 = 6;
• flyde m = y1/x1;
• int y = 0;
• float e = 0;
• plot (0, 0);
• for (int x = 1; x <= x1; x ++) {
• e+= m;
• hvis (e> = 0,5) {
• e -= 1;
• y ++;
• }
• plot (x, y);
• }

Tabel 2: Bresenhams algoritme

x	m	e	e-1	y
0	0.75	0	0	0
1	0.75	0.75	-0.25	1
2	0.75	0.5	-0.5	2
3	0.75	0.25		2
4	0.75	1	0	3
5	0.75	0.75	-0.25	4
6	0.75	0.5	-0.5	5
7	0.75	0.25		5
8	0.75	1	0	6

Hvis du undersøger algoritmen og tabel 2, vil du observere det;

• hovedsløjfen bruger kun addition og subtraktion … der er ingen multiplikation
• mønsteret for y er det samme som for tabel 1.

Men vi bruger stadig flydende tal … lad os rette dette.

Bresenhams (optimerede) algoritme

Bresenhams flydende punktalgoritme kan konverteres til en heltalsform, hvis vi skalerer 'm' og 'e' med 2*x1, i hvilket tilfælde m = (y1/x1)*2*x1 = 2*y1

Bortset fra skalering af 'm' og 'e' ligner algoritmen ovenstående bortset fra:

• vi tilføjer 2*y1 til 'e' hver gang vi øger 'x'
• vi øger y, hvis e er lig med eller større end x1.
• vi trækker 2*x1 fra 'e' i stedet for 1
• x1 bruges til sammenligning i stedet for 0,5

Algoritmens hastighed kan øges yderligere, hvis sløjfen bruger nul til testen. For at gøre dette skal vi tilføje en forskydning til fejlbetegnelsen 'e'.

• int x1 = 8;
• int y1 = 6;
• int m = (y1 << 1); // konstant: hældning skaleret med 2*x1
• int E = (x1 << 1); // konstant: 2*x1 til brug i loop
• int e = -x1; // forskydning af -E/2: test nu udført på nul
• plot (0, 0);
• int y = 0;
• for (x = 1; x <= x1; x ++) {
• e += m;
• hvis (e> = x1) {
• e -= E
• y ++;
• }
• plot (x, y);
• }

Tabel 3: Bresenhams (optimerede) algoritme

x	m	E	e	e - E	y
0	12	16	-8		0
1	12	16	4	-12	1
2	12	16	0	-16	2
3	12	16	-4		2
4	12	16	8	-8	3
5	12	16	4	-12	4
6	12	16	0	-16	5
7	12	16	-4		5
8	12	16	8	-8	6

Igen er mønsteret for y det samme som i de andre tabeller. Det er interessant at bemærke, at tabel 3 kun indeholder heltal, og at forholdet m/E = 12/16 = 0,75, som er linjens hældning 'm'.

Denne algoritme er ekstremt hurtig, da hovedsløjfen kun involverer addition, subtraktion og en sammenligning med nul. Multiplikation bruges ikke bortset fra når vi initialiserer værdierne for 'E' og 'm' ved hjælp af et "venstre-skift" for at fordoble værdierne for x1 og y1.

[1] Denne optimerede version af Bresenhams algoritme er fra et papir "Bresenham Line and Circle Drawing", copyright © 1994-2006, W Randolph Franklin (WRF). Hans materiale kan bruges til non-profit forskning og uddannelse, forudsat at du krediterer ham og linker tilbage til hans hjemmeside,

Trin 6: Koden

Download den vedhæftede fil til en mappe med samme navn, og upload den derefter til plotteren ved hjælp af dit arduino IDE (integreret udviklingsmiljø).

Afbryd HC-06 bluetoorh-modulet, før du forsøger at uploade. Dette er nødvendigt for at undgå en seriel portkonflikt med USB -kablet.

Tredjepartskode

Ud over ovenstående.ino-kode skal du bruge følgende softwarepakker, som er gratis / donations-ware:

• Teraterm, som er tilgængelig fra
• Inkscape, som er tilgængelig fra

Instruktioner til installation og brug af hver af ovenstående tredjepartspakker findes i min artikel

Trin 7: Menu

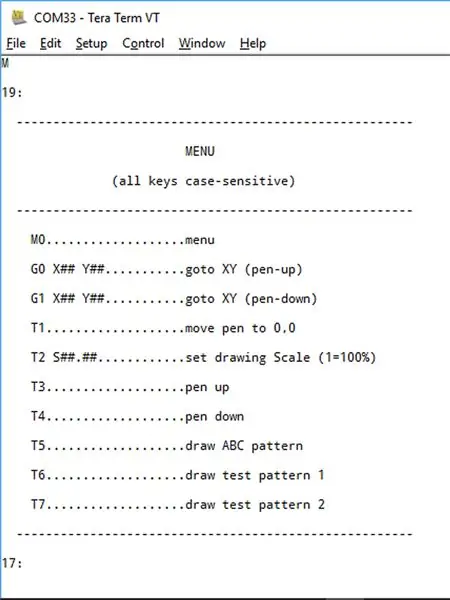
Lav en bluetooth -forbindelse med din plotter ved hjælp af "Teraterm".

Slå din "caps lock" til, da alle kommandoer er i store bogstaver.

Indtast bogstavet 'M', og en menu skal vises som vist ovenfor.

Menuen er rimeligt selvforklarende:

• M (eller M0) viser menuen
• G0 giver dig mulighed for at sende pennen til en bestemt XY-koordinat med pennen hævet.
• G1 giver dig mulighed for at sende pennen til en bestemt XY-koordinat med pennen sænket.
• T1 giver dig mulighed for at placere din pen over din 0, 0 koordinat. Skriv 'E' for at afslutte.
• T2 giver dig mulighed for at skalere din tegning. For eksempel skalerer "T2 S2.5" din tegning med 250%. Standardskalaen er 100%
• T3 og T4 giver dig mulighed for at hæve eller sænke pennen.
• T5 tegner et "ABC" testmønster.
• T6 tegner et "mål".
• T7 tegner et sæt radiale linjer, hvis formål er at kontrollere, at Bresenhams algoritme fungerer i hver af de otte "oktanter"

Bemærkninger:

• alle penbevægelser bruger tegneskalaen ved hjælp af menuindstilling T2
• "17:" og "19:" tallene er "Xon" og "Xoff" terminal håndtrykskoder fra arduino tolken.

Trin 8: Kalibrering

Værdierne for X_STEPS_PER_MM og Y_STEPS_PER_MM er for en tromle med en diameter på 90 mm.

Værdier for andre tromlediametre kan beregnes ved hjælp af følgende forhold:

• tromlens omkreds er PI*diameter
• 2048 trin svarer til en omdrejning af hver motoraksel
• en omdrejning af en GT-2 remskive svarer til 40 millimeter lineær bevægelse af et tandrem

En anden metode er at indtaste følgende kommandoer,

• G1 X0 Y100
• G1 X100 Y100

mål derefter længden af de resulterende linjer og "skala" værdierne for X-STEPS_PER_MM og Y_STEPS_PER_MM

Trin 9: Gcode -forbehandling

Denne plotter kræver kun fire af Inkscape gcodes (dvs. G0, G1, G2, G3). Koden udføres betydeligt hurtigere, hvis vi fjerner alle unødvendige gcodes og kommentarer.

For at gøre dette har du brug for en kopi af "Notepad ++". Denne gratis tekst -editor indeholder en "regulært udtryk" søgemaskine til at finde og fjerne uønsket tekst. Notesblok ++ er tilgængelig fra

Åbn den fil, der skal ændres med Notesblok ++, og placer markøren øverst i filen.

Vælg "Vis/vis symbol/alle tegn" efterfulgt af "Søg/erstat …" fra den øverste menulinje.

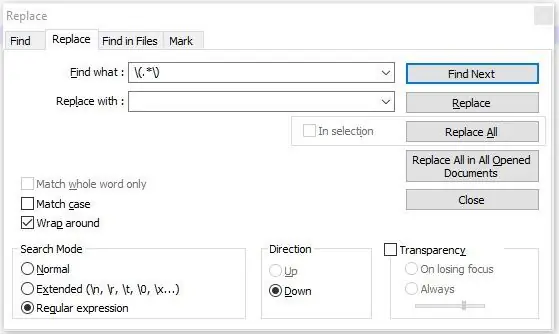
Klik på afkrydsningsfeltet "Regular Expression" (se 1. billede), og indtast hver af følgende kodesekvenser i søgefeltet.

Klik på "Erstat alle" efter hver post:

• %
• (.*)
• ^M.*$
• Z.*$

Ovenstående regulære udtryk fjerner alle % -symboler, alle kommentarer vist i parentes, alle M -koder, alle Z -koder og de følgende koder.

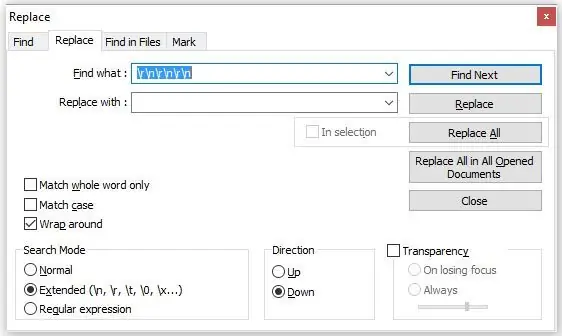
Klik nu på afkrydsningsfeltet "Udvidet udtryk" (se 2. billede), og indtast følgende kodesekvens:

r / n / r / n / r / n

Dette udtryk fjerner de uønskede vognretur og linjefeed, der er oprettet af den første sekvens.

Gem din fil under et andet navn ved hjælp af "Gem som".

Færdig.

Trin 10: Resultater

Denne plotter blev bygget som "proof of concept" og havde aldrig til hensigt at være perfekt. Når det er sagt, er resultaterne ikke så dårlige. De opfylder helt sikkert mit designmål om at overføre akvarelkonturer på papir.

De tre første billeder er de indbyggede testmønstre henholdsvis T5, T6, T7.

"Hej verden!" mønster blev sendt til plotteren via bluetooth. En "forbehandlet" kopi af denne fil er vedhæftet.

Trin 11: Kodeopdatering

Koden til denne plotter er blevet opdateret til Drum_Plotter_V2.ino.

Ændringer fra den originale Drum_Plotter.ino omfatter:

• glattere penpositionering
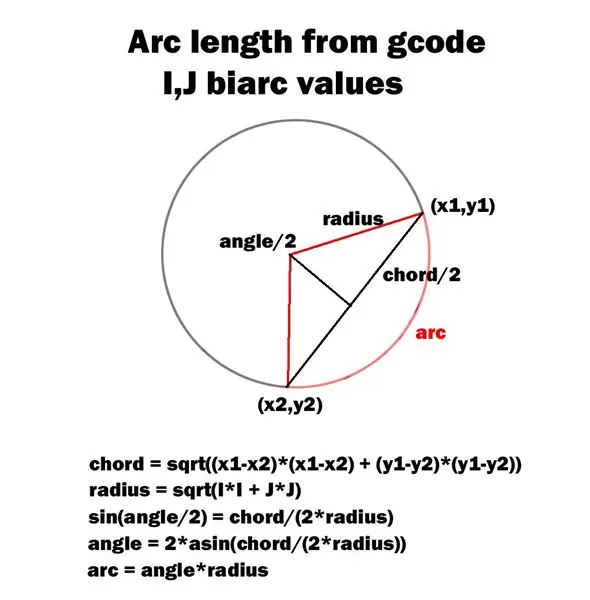
• genkender nu G02 gcode -instruktioner (buer med uret)
• genkender nu G03 gcode-instruktioner (buer mod uret)

Det vedlagte diagram skitserer min metode til beregning af buevinklen.

Trin 12: Drum_plotter_v3.ino

En kodeopdatering til "CNC Drum Plotter" er vedhæftet.

"drum_plotter_v3.ino" retter en mindre fejl, der påvirkede plotterens nøjagtighed.

Ændringshistorik

Version 2:

Bi-buekurver tilføjet

Version 3:

Følgende funktioner blev omskrevet til at løse en mindre fejl, der påvirkede plotterens nøjagtighed.

• (int) erstattet med runde () i funktionen move_to ().
• draw_line () funktion "oktant" søge algoritme forbedret
• Tolken bruger nu strengfunktioner frem for pointer, hvilket forenkler designet. For eksempel kan vi nu søge efter "MENU" frem for at lede efter bogstavet 'M' og derefter udtrække det helt tal, der følger. Dette giver dig mulighed for at personliggøre plotteren med dine egne kommandoer.

Trin 13: Drum_plotter_plotter_v4.ino

16. januar 2017:

Koden til denne tromleplotter er blevet yderligere optimeret. Yderligere funktioner er tilføjet.

Ændringerne omfatter:

• hurtigere draw_line () algoritme
• matchende move_to () -funktion
• trin tællere
• mindre fejlrettelse

For yderligere detaljer, læs kommentarerne i "drum_plotter_v4.ino" vedhæftet.

Klik her for at se mine andre instruktioner.