Indholdsfortegnelse:
- Trin 1: Forståelse af sandhedstabeller
- Trin 2: Kendskab til symbolerne
- Trin 3: Formatering af tabellen
- Trin 4: Tildel sand og falsk
- Trin 5: Negation
- Trin 6: Variabel "q"
- Trin 7: Løsning for falsk i den sidste kolonne
- Trin 8: Find det sande i den sidste kolonne
- Trin 9: Afslutning af tabellen
- Trin 10: Udført
Video: Løsning af sandhedstabeller: 10 trin

2024 Forfatter: John Day | [email protected]. Sidst ændret: 2024-01-30 08:26

En sandhedstabel er en måde at visualisere alle resultaterne af et problem. Dette instruktionssæt er lavet til folk, der kommer i gang med diskret matematik. Vi vil i dag øve os med et eksempelproblem, der er specifikt for disse instruktioner. Du skal bruge lidt ridepapir og en blyant til at visualisere bordet. Dette problem bør tage omkring 5 minutter at fuldføre for folk med forudgående viden om emnet og omkring 10 minutter for begyndere.
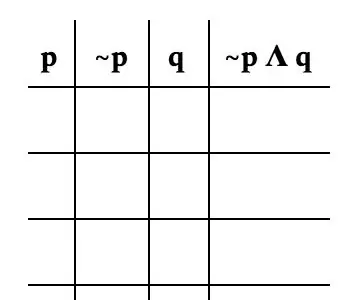
For dette instruktionssæt vil vi fokusere på problemet ~ p Λ q. Vi bruger dette til at introducere nogle symboler, der er nødvendige for at fortolke sandhedstabeller.
Trin 1: Forståelse af sandhedstabeller

En sandhedstabel er en måde at visualisere alle muligheder for et problem. At kende sandhedstabeller er en grundlæggende nødvendighed for diskret matematik. Her finder vi alle resultaterne for den simple ligning af ~ p Λ q.
Trin 2: Kendskab til symbolerne

Det første skridt til sandhedstabellen er at forstå tegnene. "~" I dette særlige problem står for negation. "P" og "q" er begge variabler. "Λ" svarer til "og". Denne ligning læses som "ikke p og q", hvilket betyder, at ligningen er sand, hvis p ikke er sand, og q er sand.
Trin 3: Formatering af tabellen

Nu for at danne den faktiske tabel. Det er vigtigt at opdele problemet med hver variabel. For dette problem vil vi opdele det som følger: p, ~ p, q og ~ p Λ q. Billedet er et godt eksempel på, hvordan dit bord skal se ud.
Trin 4: Tildel sand og falsk

Da der kun er to variabler, vil der kun være fire muligheder pr. Variabel. For p deler vi det op med halvdelen af mellemrummet taget af T (for sandt) og den anden halvdel med F (for falsk).
Trin 5: Negation

For ~ p skriver du det modsatte tegn på, at p har siden ~ p er det modsatte af p.
Trin 6: Variabel "q"

For q skifter du mellem T og F for at få hver mulig kombination. Da ligningen kun fokuserer på ~ p, kan vi ignorere p -kolonnen, når vi bestemmer sandheden i ligningen. "Λ" symbolet betyder, at både ~ p og q skal være sande for at ligningen er sand.
Trin 7: Løsning for falsk i den sidste kolonne

For den første række, da ~ p er F og q er T, ~ p Λ q er F i scenariet, at ~ p er F og q er T. Det eneste scenario ligningen er T er, hvor ~ p er T og q er T.
Trin 8: Find det sande i den sidste kolonne

Dette betyder, at den eneste række, der er T, er den tredje.
Trin 9: Afslutning af tabellen

Dobbelttjek, at dit bord er korrekt. Du gør dette ved at kontrollere, at dine skilte er rigtige og sørge for, at den sidste kolonne er udført korrekt. Den sidste kolonne er resultatet af alle de mulige permutationer fra variablerne.
Trin 10: Udført
Nu hvor du ved, hvordan du laver et grundlæggende sandhedstabel, skal du fortsætte med at øve! Jo mere du øver, jo bedre bliver du til at gøre dem.
Anbefalede:
Løsning af klikstøjsproblem på Apple 27 "skærm: 4 trin

Løsning af problem med klikstøj på Apple 27 "skærm: Har en af dine elskede skærme nogensinde begyndt at lave meget støj, når du bruger den? Dette ser ud til at ske, efter at skærmen har været i brug i flere år. Jeg debugger en af de display tænker der var en fejl fanget i køleventilatoren, b
IOT -løsning til delecyklen: 6 trin
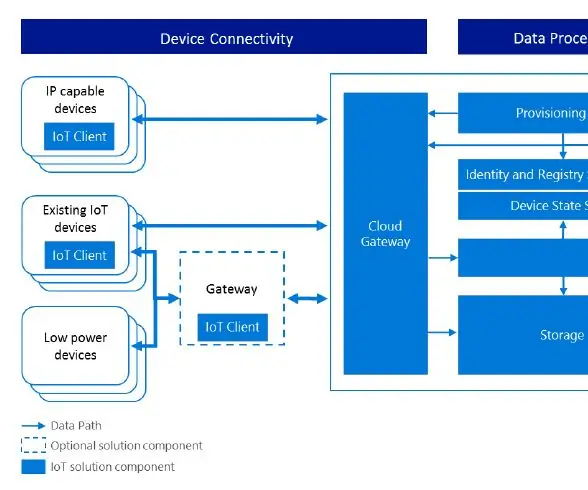
IOT -løsning til delecyklen: Delecyklen er meget populær i Kina i disse dage. Der er mere end 10 mærker til deling af cykler på markedet, og “ mobike ” er den mest berømte, den har mere end 100 millioner registrerede brugere og har spredt sig til andre byer end
En komplet Arduino roterende løsning: 5 trin

En komplet Arduino Rotary Solution: Rotary encoders er drejelige betjeningsknapper til elektroniske projekter, der ofte bruges sammen med Arduino familie mikrokontrollere. De kan bruges til at finjustere parametre, navigere i menuer, flytte objekter på skærmen, indstille værdier af enhver art. De er almindelige afløsere
Brug af fingeraftrykssensor til tidsmøde i kombination med XAMP -løsning: 6 trin (med billeder)
Brug af fingeraftrykssensor til tidsmøde i kombination med XAMP -løsning: Til et skoleprojekt ledte vi efter en løsning på, hvordan vi kan spore elevernes fremmøde. Mange af vores elever kommer sent ind. Det er et kedeligt job at kontrollere deres tilstedeværelse. På den anden side er der megen diskussion, fordi eleverne ofte vil sige
Set LoRa IoTea -løsning: 5 trin

Set LoRa IoTea -løsning: Et automatisk system til indsamling af oplysninger, der anvendes på teplantage. Det er en del af intelligent landbrugsindsamling
