Indholdsfortegnelse:
- Forbrugsvarer
- Trin 1: Opsætning
- Trin 2: Oscilloskop
- Trin 3: Beregn fase
- Trin 4: På lommeregneren
- Trin 5: Løs ligningen
- Trin 6: Beregnede værdier

Video: Komponentimpedans ved hjælp af kompleks matematik: 6 trin

2024 Forfatter: John Day | [email protected]. Sidst ændret: 2024-01-30 08:25


Her er en praktisk anvendelse af komplekse matematikligninger.
Dette er faktisk en meget nyttig teknik, som du kan bruge til at karakterisere komponenter, eller endda en antenne, ved forudbestemte frekvenser.
Hvis du har puslet med elektronik, er du måske bekendt med modstande og Ohms lov. Dvs. R = V / I Du kan nu blive overrasket over at vide, at dette også er det eneste, du skal løse for komplekse impedanser! Alle impedans er i det væsentlige komplekse, det vil sige, at de har en reel og en imaginær del. I tilfælde af en modstand er den imaginære (eller reaktans) 0, tilsvarende er der ingen faseforskel mellem V og I, så vi kan udelade dem.
En hurtig oversigt over komplekse tal. Kompleks betyder ganske enkelt, at tallet består af to dele, en reel og en imaginær. Der er to måder at repræsentere komplekse tal på. For eksempel i figuren ovenfor kan et punkt defineres af de reelle og imaginære værdier, f.eks. Hvor de gule og blå linjer mødes. For eksempel hvis den blå linje var 4 på X -aksen og 3 på Y -aksen, ville dette tal være 4 + 3i, i angiver, at dette er den imaginære del af dette tal. En anden måde at definere det samme punkt på ville være ved længden (eller amplituden) af den røde linje samt hvilken vinkel den gør med vandret. I eksemplet ovenfor ville dette være 5 <36,87.
Eller en linje med en længde på 5 i en vinkel på 36,87 grader.
I ligningen frem for alle parametrene kan R, V og I tænkes at have en imaginær del, når man arbejder med modstande, er denne værdi 0.
Når man arbejder med induktorer eller kondensatorer, eller når en faseforskel kan måles (i grader) mellem signalerne, forbliver ligningen den samme, men den imaginære del af tallet skal medtages. De fleste videnskabelige lommeregnere gør arbejdet med komplekse matematik meget let. I denne vejledning vil jeg arbejde igennem et eksempel på en Casio fx-9750GII.
Først en opsummering af modstandsspændingsdelerligningen.
I henhold til figuren -
Spændingen ved Y er strøm i ganget med R2
i er spænding X divideret med summen af R1 og R2
Når R2 er ukendt, kan vi måle de andre værdier, X, Y, R1 og omarrangere ligningen for at løse for R2.
Forbrugsvarer
Videnskabelig lommeregner
Signal generator
Oscilloskop
Trin 1: Opsætning

Lad os antage, at vi vil beregne induktansen af Device Under Test (DUT) ved 1MHz.
Signalgeneratoren er konfigureret til en sinusformet udgang på 5V ved 1MHZ.
Vi bruger 2k ohm modstande, og oscilloskop kanalerne er CH1 og CH2
Trin 2: Oscilloskop

Vi får bølgeformerne som vist på figuren. Et faseskift kan ses og måles på oscilloskopet til at føre med 130ns. Amplituden er 3,4V. Bemærk, signalet på CH1 skal være 2,5V, da det tages ved spændingsdelerens udgang, her er det vist som 5V for klarhedens skyld, da dette er den værdi, vi også skal bruge i vores beregninger. dvs. 5V er indgangsspændingen til divideren med den ukendte komponent.
Trin 3: Beregn fase

Ved 1MHz er indgangssignalets periode 1us.
130ns giver et forhold på 0,13. Eller 13%. 13% af 360 er 46,6
5V signalet får en vinkel på 0.. da dette er vores indgangssignal og faseskift er i forhold til det.
3,4V signalet får vinklen +46,6 (+ betyder, at det leder, for en kondensator ville vinklen være negativ).
Trin 4: På lommeregneren


Nu indtaster vi blot vores måleværdier i regnemaskinen.
R er 2k
V er 5 (EDIT - V er 5, senere i ligningen bruges X! Resultatet er nøjagtig det samme som jeg har X som 5 i min lommeregner)
Y er vores målte spænding med fasevinklen, dette tal indtastes som et komplekst tal, blot ved at angive vinklen som vist på lommeregnerens skærm
Trin 5: Løs ligningen

nu ligningen
(Y * R) / (X - Y)
er skrevet i lommeregneren, er dette nøjagtig den samme ligning, som vi bruger til at løse modstandsspændingsdelere:)
Trin 6: Beregnede værdier


Lommeregneren gav resultatet
18 + 1872i
Den 18, er den reelle del af impedansen, og den har en induktans på +1872 ved 1MHz.
Hvilket fungerer til 298uH ifølge induktorimpedansligningen.
18 ohm er højere end den modstand, der ville blive målt med et multimeter, det skyldes, at multimeteret måler modstand ved DC. Ved 1MHz er der hudeffekt, hvor den indre del af lederen omgås af strømmen, og den flyder kun på ydersiden af kobberet, hvilket effektivt reducerer lederens tværareal og øger dens modstand.
Anbefalede:
DIY -- Sådan laver du en edderkoprobot, der kan kontrolleres ved hjælp af smartphone ved hjælp af Arduino Uno: 6 trin

DIY || Sådan laver du en edderkoprobot, der kan styres ved hjælp af smartphone Brug af Arduino Uno: Mens du laver en edderkoprobot, kan man lære så mange ting om robotik. Ligesom at lave robotter er underholdende såvel som udfordrende. I denne video vil vi vise dig, hvordan du laver en Spider -robot, som vi kan betjene ved hjælp af vores smartphone (Androi
Kontrol ledt over hele verden ved hjælp af internet ved hjælp af Arduino: 4 trin

Kontrol ledt over hele verden ved hjælp af internet ved hjælp af Arduino: Hej, jeg er Rithik. Vi kommer til at lave en internetstyret LED ved hjælp af din telefon. Vi kommer til at bruge software som Arduino IDE og Blynk.Det er enkelt, og hvis det lykkedes dig, kan du styre så mange elektroniske komponenter, du ønskerTing We Need: Hardware:
Sådan laver du en drone ved hjælp af Arduino UNO - Lav en quadcopter ved hjælp af mikrokontroller: 8 trin (med billeder)

Sådan laver du en drone ved hjælp af Arduino UNO | Lav en Quadcopter ved hjælp af mikrokontroller: Introduktion Besøg min Youtube -kanal En Drone er en meget dyr gadget (produkt) at købe. I dette indlæg vil jeg diskutere, hvordan jeg gør det billigt ?? Og hvordan kan du lave din egen sådan til en billig pris … Nå i Indien alle materialer (motorer, ESC'er
RF 433MHZ radiostyring ved hjælp af HT12D HT12E - Lav en RF -fjernbetjening ved hjælp af HT12E & HT12D med 433mhz: 5 trin

RF 433MHZ radiostyring ved hjælp af HT12D HT12E | Oprettelse af en RF -fjernbetjening ved hjælp af HT12E & HT12D med 433mhz: I denne instruktør vil jeg vise dig, hvordan du laver en RADIO -fjernbetjening ved hjælp af 433mhz sendermodtagermodul med HT12E -kode & HT12D -dekoder IC.I denne instruktive kan du sende og modtage data ved hjælp af meget meget billige KOMPONENTER SOM: HT
Trådløs fjernbetjening ved hjælp af 2,4 GHz NRF24L01 -modul med Arduino - Nrf24l01 4 -kanals / 6 -kanals sender modtager til Quadcopter - Rc Helikopter - Rc -fly ved hjælp af Arduino: 5 trin (med billeder)
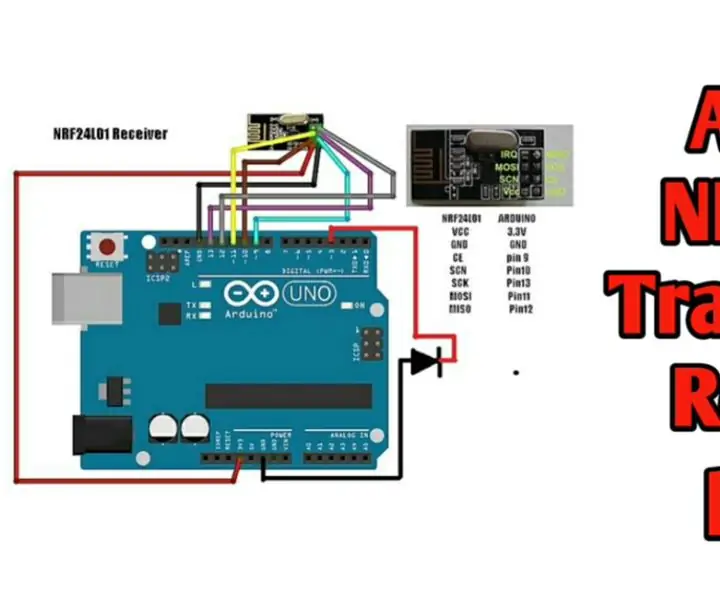
Trådløs fjernbetjening ved hjælp af 2,4 GHz NRF24L01 -modul med Arduino | Nrf24l01 4 -kanals / 6 -kanals sender modtager til Quadcopter | Rc Helikopter | Rc -fly ved hjælp af Arduino: At betjene en Rc -bil | Quadcopter | Drone | RC -fly | RC -båd, vi har altid brug for en modtager og sender, antag at vi til RC QUADCOPTER har brug for en 6 -kanals sender og modtager, og den type TX og RX er for dyr, så vi laver en på vores
