Bioimpedansanalyse (BIA) Med AD5933: 9 trin

2024 Forfatter: John Day | [email protected]. Sidst ændret: 2024-01-30 08:27

Jeg har været interesseret i at lave en bioimpedansanalysator til målinger af kropssammensætning, og mine tilfældige søgninger blev ved med at finde et design fra klassen Biomedical Instrumentation fra 2015 på Vanderbilt University. Jeg har gennemarbejdet designet og forbedret det lidt. Jeg vil gerne dele mine fund med dig. Tag det, du kan bruge fra denne "gennemgang", hvis noget ikke er klart, foreslår forbedringer. Jeg ville måske engang skrive min tanke op i en mere sammenhængende form, men for nu håber jeg, at du kan bruge det, du ser her. (Hvis du tror, du kan skrive dette op og forbedre det, er du velkommen)

Bamse

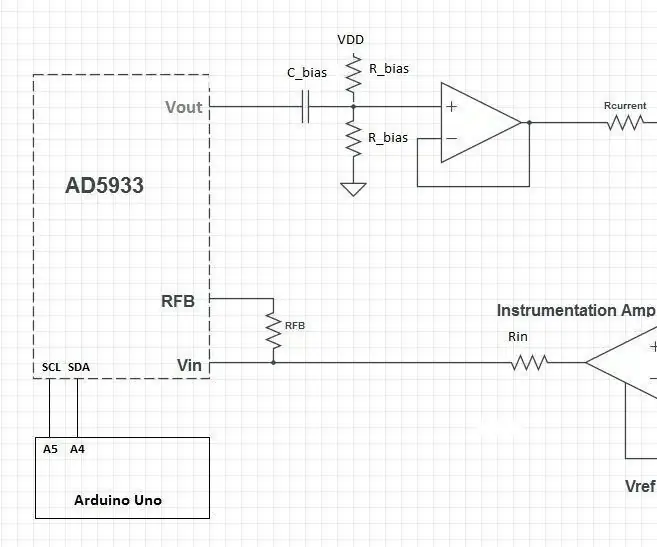
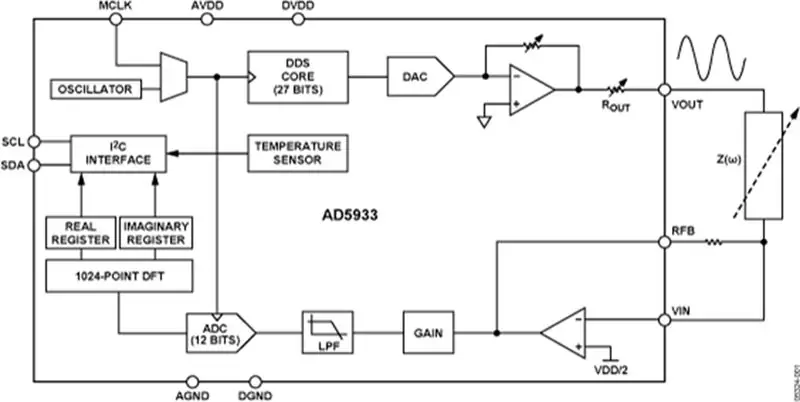
Dette design består af AD5933-chippen og en brugerdefineret analog front-end (AFE) for at grænseflade AD5933 med kroppen. AD5933 måler derefter, og resultaterne kan derefter behandles af en mikrokontroller (f.eks. En Arduino).

Hvis du planlægger at bruge Arduino som en strømforsyning, skal du sørge for, at drifts- og instrumenteringsforstærkere (op-ampere og in-ampere) understøtter såkaldte "single supply" -spændinger og har rail-to-rail-specifikationer.

(I det følgende vil jeg bruge en strømforsyning (fra en Arduino) på 5V og indstilling for område 1 på AD5933.)

Trin 1: Re-bias-fasen

Den første del af AFE er en re-bias-fase. Udgangsspændingssignalet er ikke centreret i midten af forsyningsspændingsområdet (VDD/2). Dette korrigeres ved at bruge en kondensator til at blokere DC -delen af signalet og sende det gennem en spændingsdeler for at tilføje en DC -forskydning tilbage i signalet.

De to re-bias modstande kan have en hvilken som helst værdi, så længe de er de samme. Den specifikke værdi af hætten er heller ikke vigtig.

Re-bias-stadiet fungerer som et højpasfilter og har derfor en afbrydelsesfrekvens:

f_c = 1 / (2 * pi * (0,5 * R) * C)

Sørg for, at cutoff -frekvensen er et par årtier under den minimumsfrekvens, du planlægger at bruge. Hvis du planlægger at bruge 1 kHz i din applikation, skal du gå efter hætter og modstandsværdier, der giver dig en afbrydelsesfrekvens i størrelsesordenen 1-10 Hz.

Den sidste del af dette trin er en op-amp opsat til at være en spændingsfølger. Dette er for at sikre, at modstandsværdierne ikke forstyrrer det næste trin

Trin 2: Strømfølermodstand

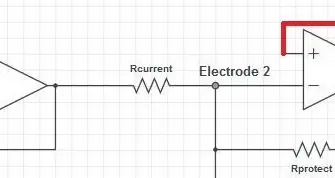
Den første del af det næste trin er den aktuelle sensormodstand. Strømmen gennem denne modstand vil være den samme strøm, som forstærkeren vil forsøge at opretholde gennem kroppen. Sørg for, at strømmen overholder IEC6060-1-sikkerhedsstandarderne*:

Under frekvenser på 1 kHz er maksimalt 10 microAmps (RMS) tilladt gennem kroppen. Ved frekvenser over 1 kHz giver følgende ligning den maksimalt tilladte strøm:

Maks. Vekselstrøm <(minimumsfrekvens i kHz) * 10 mikroAmps (RMS)

Forholdet mellem spidsamplituden for et AC -signal og dets RMS -værdi er: Peak = sqrt (2) * RMS. (10 microAmps RMS svarer til 14 microAmps maksimal amplitude)

Ved hjælp af Ohms Law om modstanden kan vi beregne den modstandsværdi, der overholder sikkerhedsstandarden. Vi bruger excitationsspændingen fra AD5933 og den maksimale strømværdi:

U = R * I => R = U / I

F.eks. ved hjælp af Range 1 -indstillingen Upeak = 3V / 2 = 1,5V (eller 1V @3,3V)

Ved at bruge 14 microAmp -spidsværdien ovenfra får jeg en modstandsværdi på mindst 107kOhms

Referencer:

* Analoge enheder: "Bio-impedans kredsløbsdesign til kropsslidte systemer"

Trin 3: Trans-konduktansforstærkeren

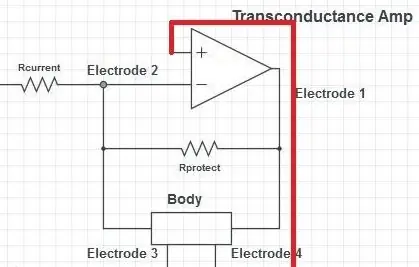
Efter den aktuelle registreringsmodstand er der en op-amp i en negativ feedback-konfiguration. Dette er en såkaldt Load-in-the-Loop-opsætning. Op-ampens positive indgangsterminal er forbundet til en VDD/2-spænding. Op-amp vil nu forsøge at justere sin output i den modsatte retning til excitationssignalet, således at spændingen ved den negative terminal vil være lig med VDD/2. Dette vil producere et vippepotentiale, der skubber og trækker strømmen gennem kroppen.

Strømmen fra op-ampens negative terminal er praktisk talt nul. Al strømmen gennem den strømfølende modstand skal derfor flyde gennem kroppen. Dette er mekanismen, der gør denne opsætning til en trans-konduktansforstærker (også kaldet en spændingsstyret strømkilde, VCCS).

Op-amp kan kun opretholde strømmen, hvis kroppens impedans ikke er for høj. Ellers ville op-amp udgangen bare maksimere ved forsyningsspændingen (0 eller 5 V). Det maksimale spændingsspænd, der kan opretholdes, er VDD/2 + Upeak (2,5 + 1,5V = 4V @ 5V forsyning). Op-ampens spændingsmargener skal trækkes fra denne værdi, men hvis op-amp'eren har rail-to-rail-specifikationer, ville det kun være en lille mængde. Den maksimale impedans, som op-amp kan drive, er derfor:

Z <(VDD / 2 + Upeak) / Imax

(I mit setup Z <4V / 14 microAmps = 285 kOhms er ønsket rigeligt til at dække kroppens impedansområde)

Beskyttelsesmodstanden har en meget stor værdi (1-1,5 MOhms) i forhold til kroppen (ca. 100kOhms), og for alle normale operationer vil dette ikke trække nogen mærkbar strøm, og impedansen for den parallelle forbindelse domineres af kroppens impedans. Hvis kroppens impedans skulle stige (f.eks. Puder, der løsner), kan strømmen derefter gå gennem modstanden, og maksimering af op-amp ville ikke skabe ubehagelige spændinger i puderne.

Trin 4: Instrumenteringsforstærkeren

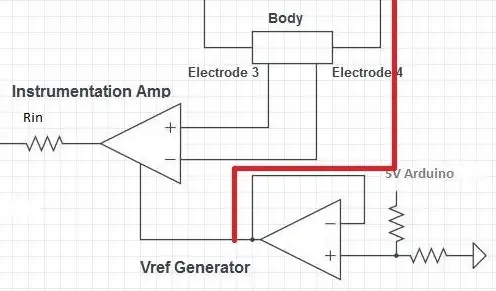
Det næste trin er instrumenteringsforstærkeren (in-amp), der måler spændingen over kroppen. Spændingen over kroppen svinger omkring 0V, men AD5933 har brug for indgangsspændingen for at være i et positivt område. In-amp tilføjer derfor en DC-forskydning af VDD/2 til det målte spændingssignal.

VDD/2 -referencen genereres af en spændingsdeler. Enhver værdimodstand kan bruges, så længe de er ens. Spændingsdeleren adskilles fra impedansen for resten af kredsløbet af en spændingsfølger. Spændingsfølgerens output kan derefter videresendes til både forstærkeren og trans-konduktansforstærkeren.

Trin 5: Inputfasen og kalibreringen

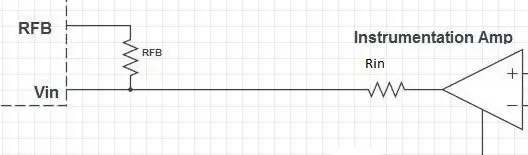
Indgangstrinnet i AD5933 indeholder en op-amp i negativ feedback-konfiguration. Der er to modstande: en i serie (Rin) og en parallelt (RFB). Op-forstærkerens forstærkning er givet ved

A = - RFB / Rin

Gevinsterne ved input op-amp og in-amp (og PGA) skal sikre, at signalet, der går ind i ADC på AD5933, altid er inden for 0V og VDD.

(Jeg bruger en enhedsforstærkning in-amp og modstandsværdier, der giver ca. A = 0,5)

Inde i AD5933 konverterer ADC spændingssignalet til a til et digitalt signal. Spændingsområdet fra 0V til VDD konverteres til det digitale område 0-128 (2^7). (Dokumentationen er ikke klar om dette, men en grundig undersøgelse af plots i [1] og nogle eksperimenter fra min side bekræfter dette.)

Inde i DFT -modulet er der en anden skalering på 256 (1024/4, se [1]), før resultatet gemmes i det virkelige og imaginære register.

Ved at følge spændingssignalet gennem AFE, ind i ADC'en og bruge skalafaktorerne nævnt før, er det muligt at estimere forstærkningsfaktoren til at være:

g = (VDD * Rstrøm * Rin) / (256 * PGA * Upeak * RFB * 2^7)

nogle kalibreringer kan stadig være nødvendige, så tag højde for nogle effekter, der ikke er en del af denne matematiske model, så mål venligst den sande forstærkningsværdi ved at måle komponenter med kendt impedans, som modstande. (g = Z / mag, se nedenfor)

Impedansen kan nu beregnes med

Z = g * mag

mag = sqrt (ægte^2 + imaginær^2)

PA = arctan2 (ægte, imaginær) - deltaPA

PA skal sandsynligvis kalibreres, og der er et systematisk faseforskydning som funktion af frekvens i AD5933. deltaPA vil sandsynligvis være en lineær frekvensfunktion.

Modstanden og reaktansen kan nu beregnes ved

R = Z * cos (PA)

X = Z * sin (PA)

Referencer: [1] Leonid Matsiev, "Forbedring af ydeevne og alsidighed af systemer baseret på enkeltfrekvente DFT-detektorer såsom AD5933", Electronics 2015, 4, 1-34; doi: 10.3390/electronics4010001

Trin 6: Advanced Stuff: Spectral Leakage (DC)

Signalet, som vi lægger ind i AD5933, er en spænding/strøm som en funktion af tiden, men vores største interesse er impedansen som en funktion af frekvens. For at konvertere mellem tidsdomæne og frekvensdomæne skal vi tage Fourier-transformen af tidsdomænesignalet. AD5933 har et indbygget diskret Fourier transform (DFT) modul. Ved lave frekvenser (under ca. 10 kHz) påvirkes indbygningen i DFT af aliasing og spektrale lækager. I [1] gennemgår han matematikken om, hvordan man retter den spektrale lækage. Essensen i dette er at beregne fem (plus to) konstanter for hvert frekvens trin i fejningen. Dette kan let gøres f.eks. af Arduino i software.

Lækagen findes i to former: en DC -lækage, der er additiv i naturen og en AC -lækage, der er multiplikativ i naturen.

DC -lækagen stammer fra det faktum, at spændingssignalet ved ADC ikke svinger omkring 0V, men omkring VDD/2. Et DC -niveau på VDD/2 skal svare til en digital DC -aflæsning på ca. 64 (betegnet delta i [1]).

Trinene til at korrigere DC -spektral lækage:

1) Beregn kuvertfaktor E for den aktuelle frekvens.

2) Beregn de to forstærkningsfaktorer GI (reel) og GQ (imaginær)

3) Træk delta * GI fra værdien af det reelle register og delta * GQ fra værdien af det imaginære register

Referencer:

[1] Leonid Matsiev, "Forbedring af systemers ydeevne og alsidighed baseret på

Enkeltfrekvente DFT-detektorer såsom AD5933 , Electronics 2015, 4, 1-34; doi: 10.3390/electronics4010001

[2] Konrad Chabowski, Tomasz Piasecki, Andrzej Dzierka, Karol Nitsch, "Simple Wide Frequency Range Impedance Meter Baseret på AD5933 Integrated Circuit", Metrol. Mål. Syst., Bind. XXII (2015), nr. 1, s. 13–24.

Trin 7: Avancerede ting: Spektral lækage (AC)

Ligesom DC -lækagen kan AC -lækagen rettes matematisk. I [1] kaldes modstanden og reaktansen henholdsvis A*cos (phi) og A*sin (phi), hvor A svarer til størrelsen af impedansen og phi svarer til fasevinklen (PA).

Trinene til at korrigere AC -spektral lækage:

1) Beregn kuvertfaktor E (ikke den samme som for DC) for den aktuelle frekvens.

2) Beregn de tre faktorer a, b og d. (ca. værdier ved højere frekvenser: a = d = 256 og b = 0)

3) Modstand (Acos (phi)) og reaktans (Asin (phi)) kan nu beregnes i digitale enheder

Referencer: [1] Leonid Matsiev, "Forbedring af ydeevne og alsidighed af systemer baseret på enkeltfrekvente DFT-detektorer såsom AD5933", Electronics 2015, 4, 1-34; doi: 10.3390/electronics4010001

[2] Konrad Chabowski, Tomasz Piasecki, Andrzej Dzierka, Karol Nitsch, "Simple Wide Frequency Range Impedance Meter Baseret på AD5933 Integrated Circuit", Metrol. Mål. Syst., Bind. XXII (2015), nr. 1, s. 13–24.

Trin 8: Avancerede ting: den teoretiske gevinstfaktor

I betragtning af den matematiske modellering af DFT bør det også være muligt at modellere hele AFE matematisk. Matematisk kan spændingssignalet beskrives ved en sinusfunktion med en given fast frekvens, en DC -forskydning og en AC -svingning med en spidsamplitude. Frekvensen ændres ikke under et frekvenstrin. Da forstærkningsfaktoren kun ændrer størrelsen af impedansen og ikke PA, vil vi her ikke være bekymrede for noget faseskift induceret på signalet.

Her er en kort opsummering af spændingssignalet, når det spreder sig gennem AFE:

1) Efter re-bias-fasen er AC-amplituden stadig upeak = 1,5V (1V @ VDD = 3,3V), og DC-forskydningen er blevet ændret til VDD/2.

2) I den aktuelle registreringsmodstand er spændingen stille den samme som det foregående trin …

3) … men på grund af vippens spænding på op-amp har AC-svingningerne en størrelse på Z*Upeak/Rcurrent. (DC -forskydningen annulleres af op -ampere -referencespændingen for VDD/2 - vippens drejepunkt - og bliver en kraftig jord i denne del af kredsløbet)

4) Enhedsforstærkeren tilføjer DC-forskydningen for VDD/2 tilbage og videresender signalet til indgangstrinnet i AD5933

5) Op-amp i inputfasen har en forstærkning på A = -RFB/Rin, og AC-amplituden bliver derfor (Z*Upeak/Rcurrent)*(RFB/Rin)

6) Lige før ADC'en er der en programmerbar forstærkerforstærker (PGA) med to indstillinger en forstærkning på 1 eller 5. Spændingssignalet ved ADC'en bliver derfor: PGA*(Z*Upeak/Rcurrent)*(RFB/Rin)

ADC konverterer v (t) signalet til et digitalt signal x (t) = u (t) / VDD * 2^7 med en 12 bit nøjagtighed.

Størrelsen A er forbundet med impedansen Z med forstærkningsfaktoren, k, som A = k * Z og har en omtrentlig værdi på k = PGA * Upeak * RFB * 2^7 / (VDD * Rstrøm * Rin).

Hvis du kan lide at arbejde med gain-faktor i stedet g = 1 / k og Z = g * A.

Trin 9: Avancerede ting: PA -skiftet

I [2] finder de et systematisk skift i PA som en funktion af frekvens. Dette skyldes en tidsforsinkelse mellem DAC'en, hvor excitationssignalet genereres, og DFT'en, hvor det indgående signal skal indvikles med det udgående signal.

Skiftet er kendetegnet ved antallet af urcyklusser, signalet er forsinkelse mellem DAC og DFT internt i AD5933.

Referencer: [1] Leonid Matsiev, "Forbedring af ydeevne og alsidighed af systemer baseret på enkeltfrekvente DFT-detektorer såsom AD5933", Electronics 2015, 4, 1-34; doi: 10.3390/electronics4010001

[2] Konrad Chabowski, Tomasz Piasecki, Andrzej Dzierka, Karol Nitsch, "Simple Wide Frequency Range Impedance Meter Baseret på AD5933 Integrated Circuit", Metrol. Mål. Syst., Bind. XXII (2015), nr. 1, s. 13–24.