Måling af temperatur fra PT100 ved hjælp af Arduino: 6 trin (med billeder)

2024 Forfatter: John Day | [email protected]. Sidst ændret: 2024-01-31 10:18

PT100 er en modstandstemperaturdetektor (RTD), der ændrer sin modstand afhængigt af dens omgivende temperatur, den bruges i vid udstrækning til industrielle processer med langsom dynamik og relativt brede temperaturområder. Det bruges til langsomme dynamiske processer, fordi RTD'er har langsomme responstider (som jeg taler mere om senere), men er præcise og har lav drift over tid. Hvad jeg vil vise dig i denne Instructable ville ikke være op til industriel standard, men det vil udsætte dig for en alternativ måde at måle temperatur på end at bruge LM35, som mange hobbyfolk ville kende og kredsløbsteorien vist kan anvendes på andre sensorer.

Trin 1: Komponenter

1x PT100 (to ledninger)

1x Arduino (enhver model)

3x 741 driftsforstærkere (LM741 eller UA741)

1x 80ohm modstand

2x 3,9kohms modstande

2x 3.3kohms modstande

2x 8,2kohms modstande

2x 47kohms modstande

1x 5kohms potentiometer

1x to terminal strømforsyning eller 8x 1,5V AA batterier

Jeg bruger en to -tråds PT100, tre og fire -leders PT100'er vil have forskellige kredsløb. Modstandsværdierne for de fleste af disse behøver ikke at være nøjagtig de samme som ovenfor, men hvis der er et par modstande, dvs. 3,9Kohms, hvis du byttede dem til lad os sige 5k, skal du skifte begge til 5k som dengang skal være det samme. Når vi får kredsløbet, siger jeg effekten af at vælge forskellige værdier. Til operationsforstærkere (op -forstærkere) kan du bruge andre op -forstærkere, men det er dem, jeg brugte.

Trin 2: Wheatstone Bridge

Jeg skal først tale om formlen for at få temperaturen fra modstanden for PT100, før jeg taler om den første del af kredsløbet, formlen for modstanden er som følger:

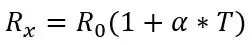
hvor Rx er PT100 -modstanden, R0 er PT100 -modstanden ved 0 grader C, α er temperaturmodstandskoefficienten og T er temperaturen.

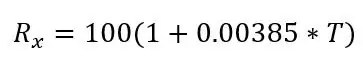
R0 er 100 ohm, da dette er en PT100, hvis det var en PT1000, ville R0 være 1000 ohm. α er 0,00385 ohm/grader C taget fra databladet. Der er også en mere præcis formel, der kan findes her, men ovenstående formel vil gøre for dette projekt. Hvis vi transponerer formlen, kan vi beregne temperaturen for en given modstand:

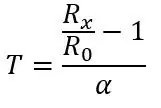
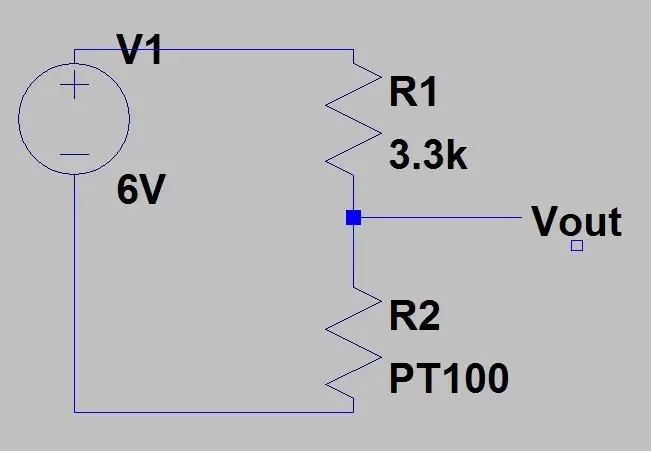
Lad os sige, at vi vil måle noget, der ville have et temperaturområde på -51,85 til 130 grader C, og vi placerede PT100 i kredsløbet vist på billede 1. Brug ligningen ovenfor og ligningen for spændingen ud af en spændingsdeler (vist i det første billede) kan vi beregne spændingsområdet. Bunden af området T = -51,85 (80ohms)

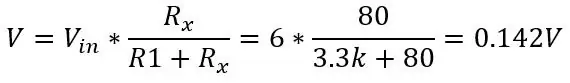
og ved 130 grader (150 ohm):

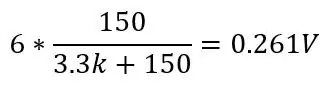
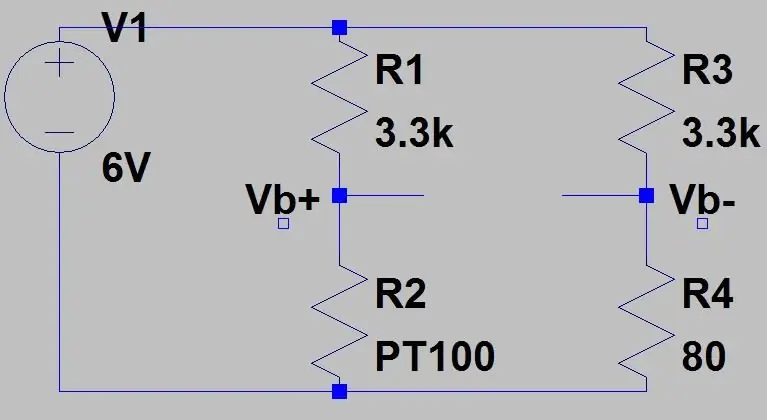
Dette ville give en rækkevidde på 0.1187V og en DC -forskydning på 0.142, fordi vi ved, at vores temperatur aldrig vil komme under -51.85 grader C, dette vil reducere følsomheden i det område, vi bekymrer os om (80 til 130 ohm), når vi forstærker denne spænding. For at slippe af med denne DC -forskydning og øge vores følsomhed kan vi bruge en Wheatstone -bro, der er vist på det andet billede.

Udgangen fra den anden spændingsdeler (Vb-) trækkes senere fra den første spændingsdelerudgang (Vb+) ved hjælp af en differentialforstærker senere. Formlen for broens output er kun to spændingsdelere:

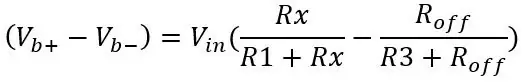
Spændingen ude for PT100 er 80 ohm og bruger de andre værdier på billedet:

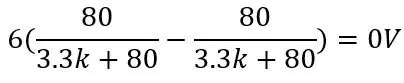
og for Pt100 er 150 ohm:

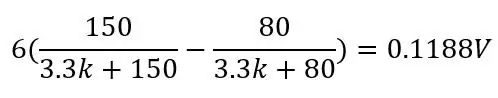
Ved at bruge Wheatstone slipper vi for DC -forskydningen og øger følsomheden efter forstærkning. Nu hvor vi ved, hvordan Wheatstone -broen fungerer, kan vi tale om, hvorfor vi bruger 80ohms og 3.3kohms. 80ohms forklares på en måde ud fra formlen ovenfor, vælg denne værdi (vi kalder dette offset -modstanden Roff) for at være det nederste område af din temperatur eller endnu bedre, lidt under bunden af dit område, hvis dette bruges til et kontrolsystem til temperaturregulering eller sådan noget, vil du gerne vide, hvor lav temperaturen kommer under dit temperaturområde. Så hvis -51,85C er bunden af dit område, skal du bruge 74,975 ohm (-65 grader C) til dit Roff.

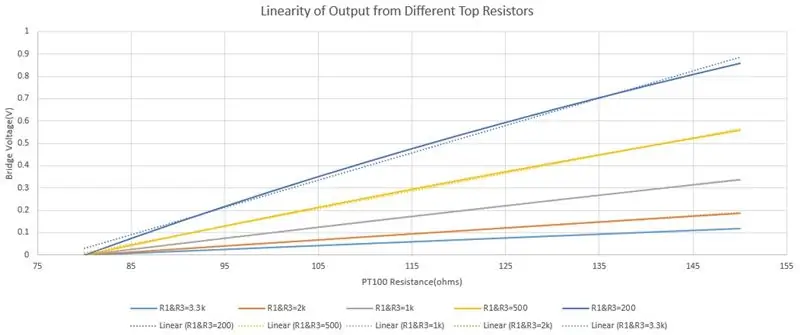
Jeg valgte 3.3k for R1 og R3 af to grunde, for at begrænse strømmen og øge outputets linearitet. Da PT100 ændrer modstand på grund af temperatur, vil for meget strøm gennem den give forkerte aflæsninger på grund af selvopvarmning, så jeg valgte en maksimal strøm på 5-10mA. Når PT100 er 80ohms er strømmen 1.775mA så sikkert under maks. Område. Du reducerer modstanden for at øge følsomheden, men dette kan have en negativ effekt på lineariteten, da vi senere vil bruge ligningen for en linje (y = mx+c), der har et ikke-lineært output, vil indføre fejl. Det tredje billede har en graf over broudgangen ved hjælp af forskellige topmodstande, den heltrukne linje er den faktiske output og den stiplede linje er den lineære tilnærmelse. Du kan se i den mørkeblå graf (R1 & R3 = 200ohms) giver det største spændingsområde, men udgangen er den mindst lineære. Den lyseblå (R1 & R3 = 3,3kohms) giver det mindste spændingsområde, men den stiplede linje og den heltrukne linje overlapper hinanden, hvilket viser, at dens linearitet er meget god.

Du er velkommen til at ændre disse værdier, så de passer til din applikation, også hvis du ændrer spændingen, skal du sørge for, at strømmen ikke bliver for høj.

Trin 3: Forstærkning

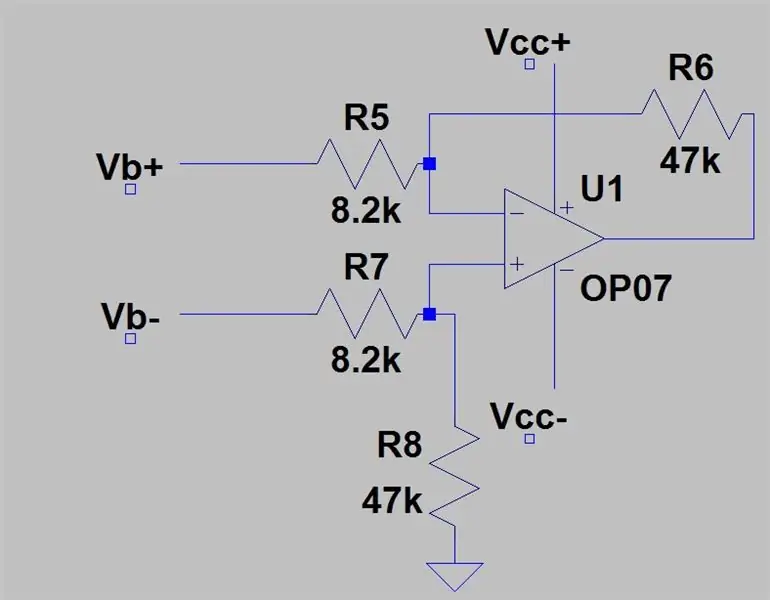
I det sidste trin fandt vi, at outputområdet for de to spændingsdelere, der blev trukket fra, var 0 til 0,1187, men vi har ikke talt om, hvordan man skal trække disse spændinger fra. For at gøre dette har vi brug for en differentialforstærker, som vil trække det ene input fra det andet og forstærke dette med forstærkerens forstærkning. Kredsløbet til en differentialforstærker er vist på det første billede. Du føder Vb+ til den inverterende indgang og Vb- i den ikke-inverterende indgang, og udgangen er Vb+- Vb- med en forstærkning på en dvs. ingen forstærkning, men ved at tilføje modstandene vist på billedet tilføjer vi en forstærkning på 5,731. Gevinsten er givet ved:

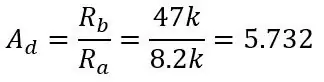
Ra er R5 & R7 og Rb er R6 & R8, spændingen ud er givet ved:

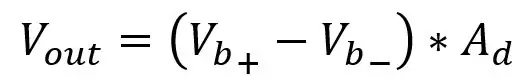
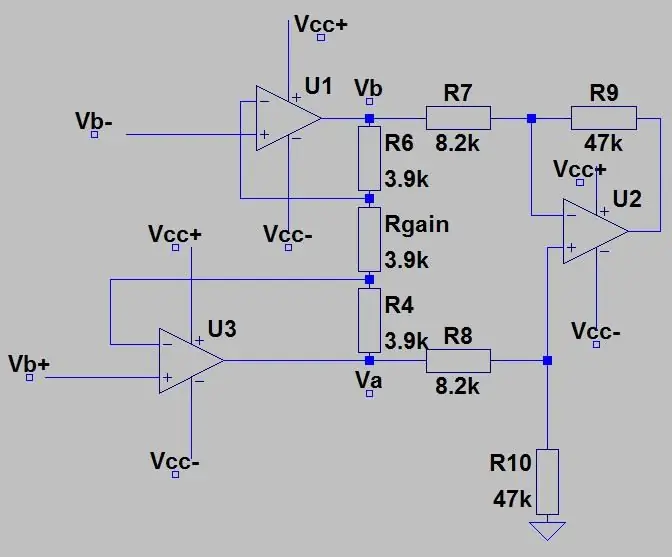
Der er to problemer med bare at tilslutte denne forstærker til broens output, indlæsningseffekten og ændring af forstærkningen. Hvis du ændrer forstærkerens forstærkning, skal du ændre mindst to modstande, da de to par modstande skal være ens, så at have to gryder, der skal have den samme værdi, ville være irriterende, så vi vil bruge noget, der kaldes en instrumenteringsforstærker som jeg taler om herunder. Belastningseffekten er indgangsmodstandene i forstærkeren, der påvirker spændingsfaldet over PT100, vi vil have spændingen over PT100 til at være uændret, og for at gøre dette kan vi vælge meget store modstande til indgangsmodstandene, så PT100's parallelle modstand og indgangsmodstand er meget tæt på PT100 -modstanden, men dette kan forårsage problemer med støj og spændingsudgangskompensation, som jeg ikke vil gå ind på. Bare vælg mellemområde i Kohms -området, men som jeg sagde, er det også dårligt at have små modstande, så vi ændrer kredsløbet lidt.

I det andet billede har vi output fra broen forbundet til en instrumenteringsforstærker, der virker som en bufferforstærker for at adskille de to halvdele af kredsløbene (broen og forstærkning), hvilket også gør det muligt at forstærke input ved at ændre kun et potentiometer (Rgain). Gevinsten af instrumentforstærkeren er givet ved:

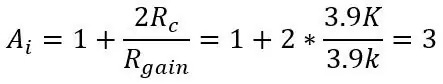
hvor Rc er de to 3,9k modstand over og under puljen.

Ved at reducere Rgain øges amplifikationen. Så på punkt Va og Vb (forstærket Vb+ og Vb-) er det bare en differentialforstærker som før, og den samlede forstærkning af kredsløbet er bare gevinsterne ganget sammen.

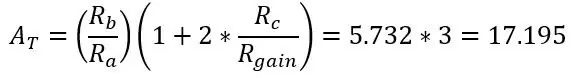
Hvis du vil vælge din gevinst, vil du gøre noget som vi gjorde før med Roff, vi bør vælge en modstand lige over din max temperatur i dit område, bare hvis det går over. Fordi vi bruger Arduino, som har en 5V adc, skal kredsløbets maksimal output være 5V ved den maksimale temperatur, du har valgt. Lad os vælge 150ohms som maks. Modstand, og brospændingen, der ikke er forstærket, var 0.1187V, den forstærkning, vi har brug for, er 42.185 (5/0.1187)

Lad os sige, at vi beholder Ra, Rb og Rc som 8,2k, 47k og 3,9k, vi skal bare finde værdien for puljen Rgain:

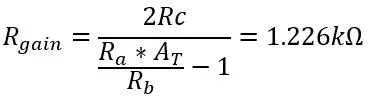
Så for at få de fulde 5 volt ud af det temperaturområde, vi bruger, skal du ændre værdien af Rgain til 1,226k. Udgangsspændingen, der kommer ud af differentialforstærkeren, er givet ved:

Trin 4: Tænd for kredsløbet

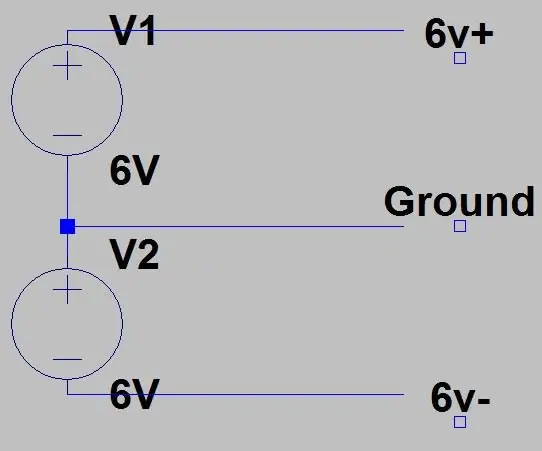
Dette er det sidste trin i kredsløbet, du har muligvis bemærket Vcc+ og Vcc- på op amp-kredsløbene, dette er fordi de har brug for både positiv og negativ spænding for at fungere korrekt, du kan få enkeltskinne op-ampere, men jeg besluttede mig at bruge denne forstærker, da det var det, jeg havde liggende. Så vi leverer +6V og -6V, der er tre måder, vi kan gøre dette på. Den første er vist på det første billede, hvor vi skal to strømforsyninger eller to udgangsterminaler fra en enkelt strømforsyning, har begge ved 6V og har en positiv udgang forbundet med den negative af den anden. 6V for topforsyningen vil være vores +6V, positiv for bundforsyningen er GND og minus for bundforsyningen er -6V. TILSLUT KUN DET SOM, HVIS GND'erne for de to forsyninger er adskilt eller det beskadiger din strømforsyning. Alle kommercielle strømforsyninger ville have adskilt GND'er, men hvis du vil kontrollere, skal du bruge kontinuitetstesteren på dit multimeter, hvis det summer, skal du ikke bruge denne opsætning og bruge den næste. På min hjemmelavede forsyning sprang jeg sikringen ved at gøre dette.

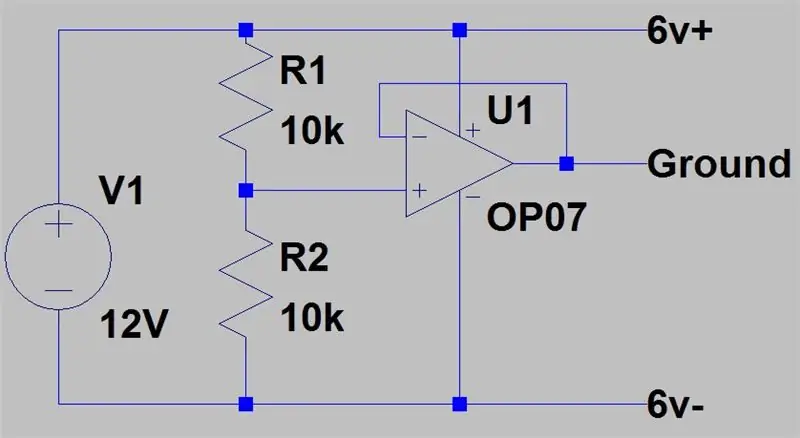
På det andet billede er det andet setup, vi kan have, det kræver en forsyning for at have dobbelt spænding fra anden, men beskadiger ikke forsyningen, hvis GND'erne er tilsluttet. Vi har to forsyninger, en ved 12V og en anden ved 6V. 12V vil fungere som vores +6V, 6V ud af den anden forsyning vil fungere som GND og de to faktiske GND'er ud af forsyningerne vil fungere som -6V.

Denne sidste opsætning er for strømforsyningerne med kun en udgang, den bruger en bufferforstærker med forstærkning 1 til at skabe en virtuel jord ved at føre halvdelen af forsyningsspændingen gennem bufferforstærkeren. Derefter fungerer 12V som +6V, og den faktiske GND -terminal er -6V.

Hvis du vil bruge batterier, vil jeg foreslå den første opsætning, men et problem med batterier er, at spændingen falder, når de begynder at dø, og spændingen ud af broen også vil falde, hvilket giver forkerte temperaturmålinger. Du kunne selvfølgelig læse spændingen fra batterierne og inkludere dem i beregningerne eller bruge regulatorer og flere batterier. I sidste ende er det op til dig.

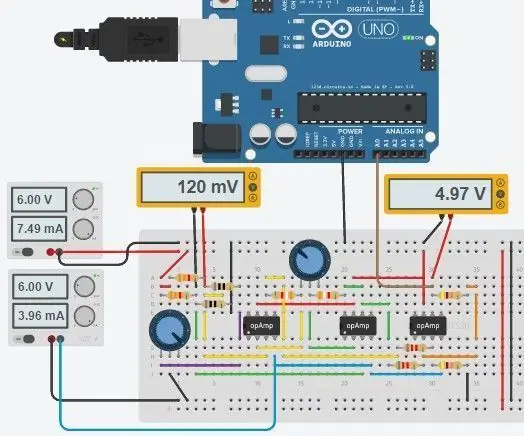
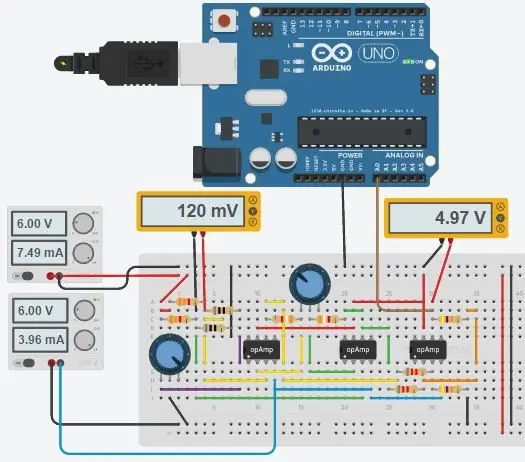
Trin 5: Fuldt kredsløb og kode

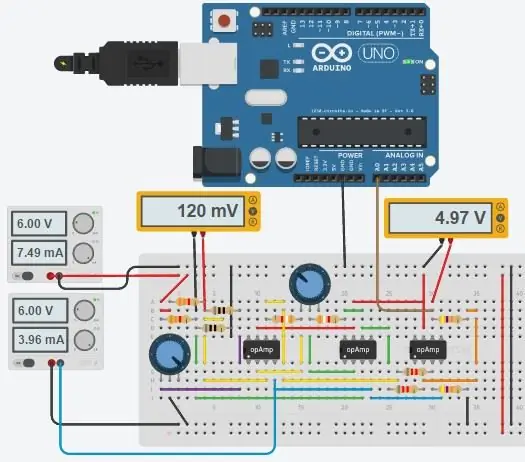
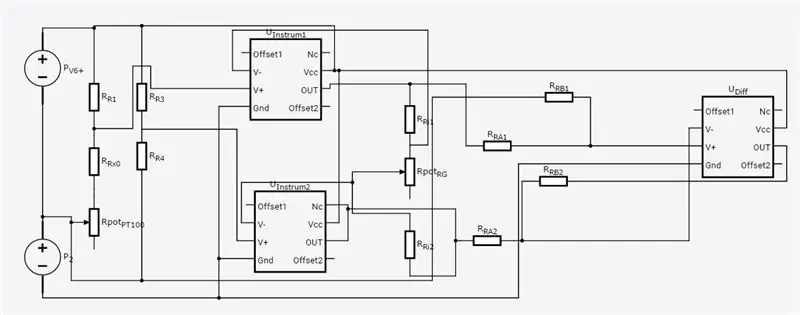
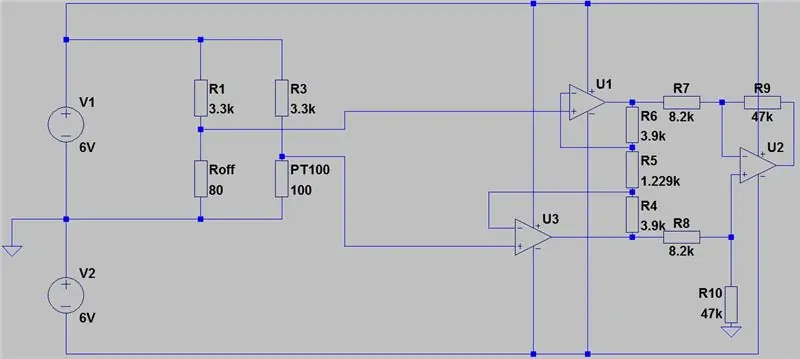
Det fulde kredsløb er vist ovenfor, og det blev lavet i Autodesks nye Circuits.io, som lader dig oprette kredsløb på brødbræt, redigere kredsløbsdiagram (vist på billede 2) og printkort og den bedste del, lader dig simulere kredsløbet fra brødbrættet og kan endda programmere en Arduino og tilslutte den i breadboard -tilstanden, længere nede på siden er simuleringen, og du kan lege med to gryder. Hvis du vil kopiere kredsløbet og indsætte dine egne værdier, kan du finde kredsløbet her. Den første gryde er 70 ohm og i serie med en 80ohm modstand, der simulerer PT100 med en rækkevidde på 80-150 ohm, den anden gryde er forstærkningen af instrumenteringsforstærkeren. Desværre brugte jeg et bibliotek, jeg downloadede til min kode, så Arduino er ikke inkluderet i kredsløbet nedenfor, men der er kun to ekstra ledninger, du skal tilslutte. Hvis du er mere fortrolig med LTspice, inkluderede jeg en asc -fil med kredsløbet.

Tilslut A0 -pin til udgangen på differentialforstærkeren

Tilslut Arduinoens GND til kredsløbets GND (IKKE -6V)

Og det er kredsløbet gjort, nu på koden. Tidligere nævnte jeg, at vi vil bruge formlen y = mx+c, ja nu skal vi beregne m (hældningen) og c (forskydningen). I Arduino læser vi spænding, men temperaturligningen har brug for, at vi kender PT100's modstand, så en måde vi kan gøre dette på er ved at udskifte Serial.println (temp) med Serial.println (V) og registrere spænding og modstand ved to temperaturer. Når du udfører denne test, skal du lade PT100 være i ro et øjeblik, som et minut eller to, og hold dig væk fra varmekilder (sollys, bærbar ventilator, din krop osv.).

Det første punkt, vi kan tage, er stuetemperatur, når du har kredsløbet tilsluttet og fungerer, skal du registrere spændingen (Vt1), der er aflæst af Arduino på den serielle skærm, og hurtigt afbryde PT100 og registrere dens modstand (Rt1), læg ikke din hænder på sonden ved frakobling, da dette vil ændre modstanden. For den anden temperatur kunne vi placere sonden i isvand eller varmt vand (vær forsigtig, hvis du bruger varmt vand) og gentag, hvad vi gjorde, før vi fandt Vt2 og Rt2. Lige efter du har placeret sonden i væsken, skal du vente et minut eller to, indtil modstanden sætter sig. Hvis du er interesseret i tidsresponsen for PT100, skal du registrere spændingen fra den serielle skærm hvert andet sekund, så kan vi tegne en graf herfra, og jeg forklarer det senere. Ved hjælp af de to spændinger og modstande kan vi beregne hældningen som følger:

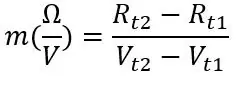
Rt1 og Rt2 er modstandene ved de to temperaturer og det samme gælder for spændingerne Vt1 og Vt2. Fra skråningen og et af de to sæt punkter, du har registreret, kan vi beregne forskydningen:

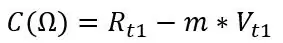
C skal være tæt på din rigtige Roff, Fra min simulering beregnede jeg disse værdier:

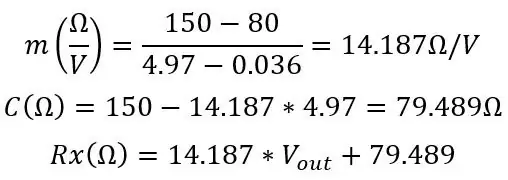
Fra denne modstand kan vi finde vores temperatur ved hjælp af formlen, vi havde i starten:

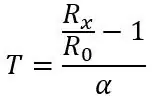
Og det er det, koden til Arduino er nedenfor. Hvis du har problemer, skal du bare efterlade en kommentar, så prøver jeg at hjælpe.

Der er ingen billeder af kredsløbet, jeg lavede, da jeg lavede det for et stykke tid siden og ikke længere har PT100 til at lave om og teste, men du skal bare tro mig på, at det virker. Der er ikke meget om PT100 på Instructables, som jeg fandt, så derfor lavede jeg denne ible.

I det næste trin vil jeg tale om tidsresponsen på PT100, og hvis du ikke er interesseret i matematik, skal du lade PT100 nøjes med et minut, før du tager aflæsningen, når du måler en temperaturændring.

Hvis du er interesseret i at se andre projekter, jeg har lavet, kan du besøge min

Blog: Roboroblog

YouTube -kanal: Roboro

Eller se på mine andre instruktioner: her

Hvis HTML roder med koden herunder, er koden vedhæftet

* Denne kode beregner temperaturen ved hjælp af en PT100

* Skrevet af Roboro * Github: <a href = "https://github.com/RonanB96/Read-Temp-From-PT100-… <a href =" https://github.com/RonanB96/Read-Temp- From-PT100-… <a href = "https://github.com/RonanB96/Read-Temp-From-PT100-… >>>>>>>>> * Circuit: <a href=" href="https://github.com/RonanB96/Read-Temp-From-PT100-… <a href=" https://github.com/ronanb96/read-temp-from-pt100-…="">>>>>>>>>> * Blog: <a href=" href="https://github.com/RonanB96/Read-Temp-From-PT100-… <a href=" https://github.com/ronanb96/read-temp-from-pt100-…="">>>>>>>>>> * Instrustable Post: <a href=" href="https://github.com/RonanB96/Read-Temp-From-PT100-… <a href=" https://github.com/ronanb96/read-temp-from-pt100-…="">>>>>>>>>> * */ //You'll need to download this timer library from here //https://www.doctormonk.com/search?q=timer #include "Timer.h" // Define Variables float V; float temp; float Rx; // Variables to convert voltage to resistance float C = 79.489; float slope = 14.187; // Variables to convert resistance to temp float R0 = 100.0; float alpha = 0.00385; int Vin = A0; // Vin is Analog Pin A0 Timer t; // Define Timer object

void setup() {

Serial.begin(9600); // Set Baudrate at 9600 pinMode(Vin, INPUT); // Make Vin Input t.every(100, takeReading); // Take Reading Every 100ms } void loop() { t.update(); // Update Timer } void takeReading(){ // Bits to Voltage V = (analogRead(Vin)/1023.0)*5.0; // (bits/2^n-1)*Vmax // Voltage to resistance Rx = V*slope+C; //y=mx+c // Resistance to Temperature temp= (Rx/R0-1.0)/alpha; // from Rx = R0(1+alpha*X) // Uncommect to convet celsius to fehrenheit // temp = temp*1.8+32; Serial.println(temp); }

Step 6: Time Response of PT100

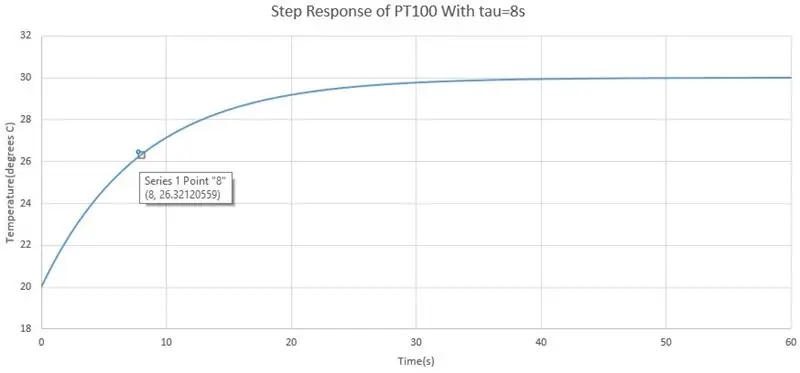
Så jeg nævnte, at PT100 reagerer langsomt, men vi kan til enhver tid få en formel for den aktuelle temperatur læst af PT100. Svaret fra PT100 er et førsteordens svar, der kan skrives i Laplace -termer, dvs. overførselsfunktion, som:

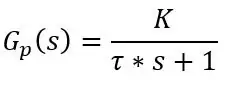
hvor tau (τ) er tidskonstanten, K er systemets forstærkning og s er Laplace -operatoren, som kan skrives som jω hvor ω er frekvens.

Tidskonstanten fortæller dig, hvor lang tid det tager et førsteordens system at afregne til sin nye værdi, og en regel eller tommelfinger er, at 5*tau er, hvor lang tid det vil tage at slå sig ned i den nye steady state. Forstærkningen K fortæller dig, hvor meget input skal forstærkes. Med PT100 er forstærkningen, hvor meget modstanden ændres divideret med temperaturændringen, fra at vælge to tilfældige værdier fra dette datablad, fik jeg en forstærkning på 0,3856 ohm/C.

Før jeg sagde, at du kunne registrere spændingen hver 2. sekund, efter at du havde sat sonden i væsken, varm eller kold, ud fra dette kan vi beregne systemets tidskonstant. Først skal du identificere, hvor startpunktet og slutpunktet er, startpunktet er spændingen, før du sætter sonden i væsken, og slutpunktet er, når det slog sig ned. Træk dem derefter, og det er spændingsændringen i trinnet, den test, du udførte, var en trinændring, som er en pludselig ændring i input til et system, hvor trin er temperatur. Gå nu til din graf til 63,2% af spændingsændringen, og denne tid er tidskonstanten.

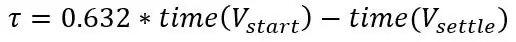
Hvis du tilslutter denne værdi til overførselsfunktionen, har du derefter formlen til at beskrive systemernes frekvensrespons, men det er ikke det, vi ønsker lige nu, vi vil have den faktiske temperatur på tidspunktet t for et trin i temperaturen, så vi går at skulle udføre en omvendt Laplace -transformation af et trin ind i systemet. Overførselsfunktionen for et førsteordens system med input af et trin er som følger:

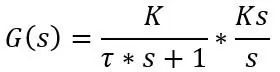
Hvor Ks er trinstørrelsen, dvs. temperaturforskellen. Så lad os sige, at sonden er afgjort ved 20 grader C, placeret i vand ved 30 grader C, og sonden har en tidskonstant på 8s, overførselsfunktionen og tidsdomæneformlen er som følger:

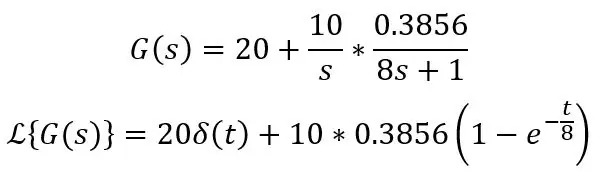
Δ (t) betyder bare en impuls, dvs. DC -forskydning på 20 grader C i dette tilfælde, du kan bare skrive 20 i dine ligninger, når du beregner dette. Dette er standardligningen for trin til et første ordens system:

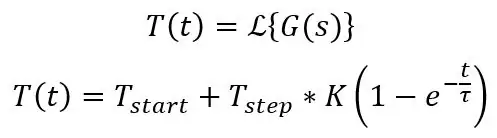
Ovenstående beregner temperaturen på tidspunktet t, men dette fungerer for spændingen, da de er proportional med hinanden, du har bare brug for start- og slutværdien, tidskonstant og trinstørrelse. Et websted kaldet Symbolab er fantastisk til at kontrollere, om din matematik er rigtig, det kan lave Laplace, integration, differentiering og masser af andre ting, og det giver dig alle trin undervejs. Den inverse Laplace -transformering af ovenstående kan findes her.