Selvbalancerende robot ved hjælp af PID -algoritme (STM MC): 9 trin

2024 Forfatter: John Day | [email protected]. Sidst ændret: 2024-01-30 08:29

For nylig er der blevet arbejdet meget med selvbalancering af objekter. Begrebet selvbalancering startede med balancering af omvendt pendul. Dette koncept omfattede også design af fly. I dette projekt har vi designet en lille model af selvbalancerende robot ved hjælp af PID (Proportional, Integral, Derivative) algoritme. Siden da er denne metode det nye ansigt for de industrielle processtyringssystemer. Denne rapport gennemgår de metoder, der er involveret i selvbalancering af objekter. Dette projekt blev udført som et semesterprojekt for at forstå sammenhængen mellem PID om effektiviteten af forskellige industrielle processer. Her fokuserer vi kun på at give en kort gennemgang af effektiviteten og anvendelsen af PID -kontrollen. Dette papir er blevet udviklet ved at give en kort introduktion til kontrolsystemer og relaterede terminologier, ud over motivationen for projektet. Eksperimenter og observationer er blevet taget, fordele og ulemper beskrevet med slutning ved de fremtidige forbedringer. En model for selvbalancerende robot blev udviklet for at forstå effektiviteten af PID i kontrolsystemets verden. Ved at gennemgå nogle strenge tests og eksperimenter blev fordele og ulemper ved PID -kontrolsystemet opdaget. Det blev konstateret, at på trods af mange fordele ved PID -kontrol over tidligere metoder, kræver dette system stadig en masse forbedringer. Det håbes, at læseren får en god forståelse af vigtigheden af selvbalancering, effektiviteten og manglerne ved PID -kontrol

Trin 1: Introduktion

Med fremkomsten af computere og industrialiseringen af processer i menneskets historie har der altid været forskning for at udvikle måder at finjustere processer og endnu vigtigere på at kontrollere dem ved hjælp af maskiner autonomt. Formålet er at reducere menneskets engagement i disse processer og derved reducere fejlen i disse processer. Derfor blev feltet "Control System Engineering" udviklet. Control System Engineering kan defineres som at bruge forskellige metoder til at styre driften af en proces eller vedligeholdelse af et konstant og foretrukket miljø, det være sig manuelt eller automatisk.

Et enkelt eksempel kunne være at kontrollere temperaturen i et rum. Manuel kontrol betyder tilstedeværelsen af en person på et sted, der kontrollerer de nuværende forhold (sensor), sammenligner den med den ønskede værdi (behandling) og tager passende handlinger for at opnå den ønskede værdi (aktuator). Problemet med denne metode er, at den ikke er særlig pålidelig, da en person er tilbøjelig til fejl eller uagtsomhed i sit arbejde. Et andet problem er også, at hastigheden af processen, der startes af aktuatoren, ikke altid er ensartet, hvilket betyder, at den nogle gange kan forekomme hurtigere end krævet, eller nogle gange kan den være langsom. Løsningen på dette problem var at bruge en mikro-controller til at styre systemet. Mikrokontrolleren er

programmeret til at styre processen i henhold til givne specifikationer, forbundet i et kredsløb (skal diskuteres senere), fodrede den ønskede værdi eller betingelser og kontrollerer derved processen for at opretholde den ønskede værdi. Fordelen ved denne proces er, at der ikke kræves nogen menneskelig indgriben i denne proces. Hastigheden af processen er også ensartet

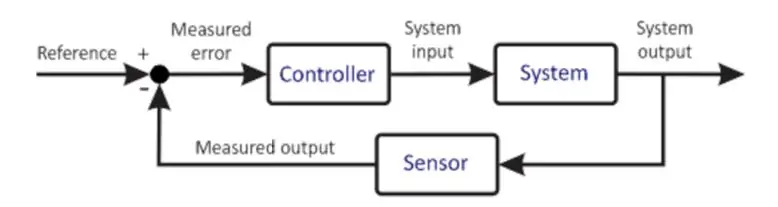
Grundlæggende kontrolsystem

Det foregående diagram viser en meget forenklet version af et kontrolsystem. Mikrocontrolleren er kernen i ethvert kontrolsystem. Det er en meget vigtig komponent, derfor bør dets valg af valg foretages omhyggeligt baseret på systemets krav. Mikrokontrolleren modtager et input fra brugeren. Denne input definerer den ønskede tilstand for systemet. Mikrocontrolleren modtager også et feedbackinput fra sensoren. Denne sensor er forbundet til systemets udgang, hvis information sendes tilbage til indgangen. Mikroprocessoren, baseret på sin programmering, udfører forskellige beregninger og giver et output til aktuatoren. Aktuatoren, baseret på output, styrer anlægget for at forsøge at opretholde disse betingelser. Et eksempel kan være en motordriver, der kører en motor, hvor motorføreren er aktuatoren, og motoren er anlægget. Motoren roterer således med en given hastighed. Den tilsluttede sensor læser anlæggets tilstand på nuværende tidspunkt og sender den tilbage til mikrokontrolleren. Mikrokontrolleren sammenligner igen, foretager beregninger og dermed gentager cyklussen sig selv. Denne proces er gentagende og endeløs, hvorved mikrokontrolleren opretholder de ønskede betingelser

Trin 2: PID -baseret kontrolsystem

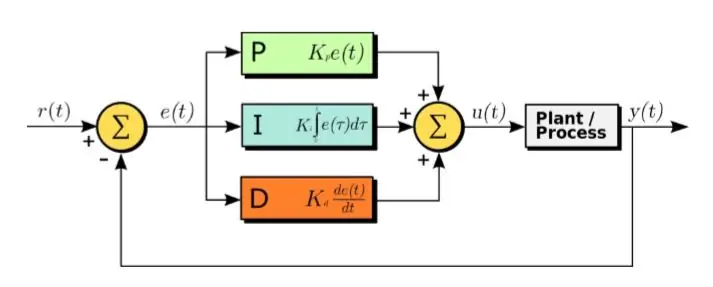
PID -algoritmen er en effektiv metode til at designe et kontrolsystem.

Definition

PID står for Proportional, Integral and Derivative. I denne algoritme er det modtagne fejlsignal input. Og følgende ligning anvendes på fejlsignalet

U (t) = Kp ∗ e (t) + Kd ∗ d/dt (e (t)) + Ki ∗ integral (e (t)) (1.1)

Kort forklaring

Som det kan ses i ligningen ovenfor, beregnes integralet og derivatet af fejlsignalerne, ganges med deres respektive konstanter og tilføjes sammen med konstanten Kp ganget med e (t). Udgangen føres derefter til aktuatoren, som får systemet til at køre. Lad os nu se på hver del af funktionen efter tur. Denne funktion påvirker direkte stigningstid, faldtid, top over skyde, afviklingstid og steady state fejl.

• Proportional del: Den proportionelle del reducerer stigningstiden og reducerer steady state fejlen. Det betyder, at systemet vil tage mindre tid at nå sin højeste værdi, og når det når sin steady state, vil steady state -fejlen være lav. Det øger imidlertid toppen overshoot.

• Afledt del: Den afledte del reducerer overskridelsen og afregningstiden. Det betyder, at systemets forbigående tilstand bliver mere dæmpet. Systemet vil også nå sin steady state på mindre tid. Det har imidlertid ingen effekt på stigningstiden eller steady state -fejlen.

• Integreret del: Den integrerede del reducerer stigningstiden og eliminerer fuldstændig fejl ved steady state. Det øger imidlertid topoverskridelsen og afregningstiden.

• Tuning: Et godt kontrolsystem har lav stigningstid, afregningstid, maksimal overskridelse og steady state fejl. Derfor skal Kp, Kd, Ki finjusteres for at justere bidraget fra ovenstående faktorer for at erhverve et godt kontrolsystem.

Der er vedhæftet figur, der viser effekten af ændring af forskellige parametre i PID -algoritmen.

Trin 3: Selvbalancerende robot

En selvbalancerende robot er en to-hjulet robot med flere lag.

Robotten vil forsøge at balancere sig selv ved anvendelse af ulige kræfter. Det vil balancere sig selv ved anvendelse af magt, der modsætter sig resultatet af kræfterne på robotten.

Metoder til selvbalancering

Der er fire metoder til selvbalancering af robotter. Disse er som følger:

Selvbalancering ved hjælp af to IR -tilt -sensor

Dette er en af de mest groveste måder at balancere robotten på, da den kræver meget mindre hardware og en relativt let algoritme. I denne tilgang bruges to vippede IR -sensorer til at måle afstanden mellem jorden og robotten. Baseret på den beregnede afstand kan PID bruges til at drive motorerne til at balancere robotten i overensstemmelse hermed. En ulempe ved denne metode er, at IR -sensoren kan gå glip af nogle aflæsninger. Et andet problem er, at en afbrydelse og sløjfer er nødvendige til beregning af afstand, hvilket øger algoritmens tidskompleksitet. Derfor er denne metode til at afbalancere robot ikke meget effektiv.

Selvbalancering ved hjælp af accelerometer

Accelerometer giver os accelerationen af kroppen i 3 akser. Acceleration orienteret i y-aksen (opad) og x-aksen (fremad) giver os målet for at beregne tyngdekraften og dermed beregne hældningsvinklen. Vinklen beregnes som følger:

θ = arctan (Ay/Ax) (1.2)

Ulempen ved at bruge denne metode er, at under robotens bevægelse vil den vandrette acceleration også blive tilføjet til målingerne, hvilket er en højfrekvent støj. Derfor vil hældningsvinklen være unøjagtig.

Selvbalancering ved hjælp af gyroskop

Et gyroskop bruges til at beregne vinkelhastighederne langs de tre akser. Hældningsvinklen opnås ved hjælp af følgende ligning.

θp (i) = θp (i − 1) + 1/6 (vali − 3 + 2vali − 2 + 2vali − 1 + vali) (1.3)

En stor ulempe ved at bruge gyroskopet er, at det har en lille DC Bias, som er en lavfrekvent støj, og på få tid er de returnerede værdier helt forkerte. Dette vil efter integration få nulpunktet til at glide væk. Som et resultat af det vil robotten forblive i sin lodrette position i et stykke tid og falde om, når driften kommer.

Selvbalancering ved hjælp af både accelerometer og gyroskop

Som diskuteret ovenfor vil brug af kun accelerometer eller gyroskop ikke give os den korrekte hældningsvinkel. For at gøre rede for det bruges både accelerometer og gyroskop. Disse er begge integreret i MPU6050. I dette får vi dataene fra dem begge og smelter dem derefter ved enten at bruge Kalman -filter eller komplementært filter.

• Kalman -filter: Kalman -filteret beregner det bedste estimat af et dynamisk systems tilstand ud fra støjende målinger og minimerer estimatets gennemsnitlige kvadratfejl. Det fungerer i to faser, forudsigelse og korrektion, givet de diskrete stokastiske ligninger, der beskriver systemdynamikken. Det er imidlertid en meget kompleks algoritme at implementere især på en begrænset hardware i en mikrokontroller.

• Komplementær filter: Denne algoritme bruger primært de data, der er hentet fra gyroskopet og integrerer det over tid for at få hældningsvinklen. Det bruger også en lille andel af accelerometermålinger. Komplementærfilter minimerer faktisk højfrekvensstøj fra accelerometer og lavfrekvent støj fra gyroskop og smelter dem derefter for at give den bedste nøjagtige hældningsvinkel.

Trin 4: Design af robot

Vi har designet en selvbalancerende robot ved hjælp af Proportional Derivative controller implementeret af komplementær filter til MPU6050. Denne lille model af Self Balancing Robot vil illustrere os nytten af kontrolsystemer i selvbalancering af robotter.

Systemimplementering:

Systemet er en selvbalancerende robot. Det implementeres ved hjælp af PID -controller, som er en proportionel integreret afledt controller. Vi afbalancerer robotten ved at køre hjulene i dens faldretning. Ved at gøre det forsøger vi at holde robotens tyngdepunkt over drejepunktet. For at køre hjulene i dens faldretning, bør vi vide, hvor robotten falder, og den hastighed, hvormed den falder. Disse data indhentes ved hjælp af MPU6050, der har et accelerometer og et gyroskop. MPU6050 måler hældningsvinklen og giver output til mikrokontrolleren. MPU6050 er forbundet med STM -kortet gennem I2C. I I2C er en ledning til uret, der er navngivet som SCL. Den anden er til dataoverførsel, som er SDA. I dette bruges master slave kommunikation. Startadresse og slutadresse er angivet for at vide, hvorfra dataene starter, og hvor de slutter. Vi har implementeret komplementærfilteret her til MPU6050, som er et matematikfilter til at flette output fra accelerometer og gyroskop. Efter at have indhentet data fra MPU6050, vil mikrokontrolleren udføre beregninger for at vide, hvor de falder. Baseret på beregningerne vil STM-mikrokontroller give kommandoer til motorføreren til at køre køretøjerne i faldretning, hvilket vil balancere robotten.

Trin 5: Projektkomponenter

Følgende komponenter blev brugt i selvbalancerende robotprojekt:

STM32F407

En mikro-controller designet af ST Microelectronics. Det fungerer på ARM Cortex-M Architecture.

Motorfører L298N

Denne IC bruges til at køre motoren. Det får to eksterne indgange. En fra mikrokontrolleren, som giver den et PWM -signal. Ved at justere bredden på pulsen kan motorhastigheden justeres. Dens anden indgang er den spændingskilde, der kræves for at drive motoren, hvilket er et 12V batteri i vores tilfælde.

DC motor

En DC -motor kører på en DC -forsyning. I dette eksperiment kører DC -motoren ved hjælp af de optokoblere, der er forbundet til motordriveren. Til at køre motoren har vi brugt motordrevet L298N.

MPU6050

MPU6050 bruges til at få information om, hvor robotten falder. Den måler hældningsvinklen i forhold til nulhældningspunktet, som er positionen for MPU6050, når programmet begynder at køre.

MPU6050 har et 3-akset accelerometer og et 3-akset gyroskop. Accelerometeret måler acceleration langs de tre akser, og gyroskopet måler vinkelhastighed omkring de tre akser. For at kombinere output skal vi filtrere lyde fra begge. For at fjerne lydene har vi Kalman og komplementær filtret. Vi har implementeret komplementærfilter i vores projekt.

Opto Par 4N35

En optokobler er en enhed, der bruges til at isolere lavspændingsdelen og højspændingsdelen af kredsløbet. Som navnet antyder, fungerer det ud fra lys. Når lavspændingsdelen får et signal, strømmer der strøm i højspændingsdelen

Trin 6: Robots struktur

Robotens struktur forklares som følger:

Fysisk struktur

Den selvbalancerende robot består af to lag, der består af gennemsigtigt plastglas. Detaljerne for to lag er angivet nedenfor:

Første lag

I den nederste del af første lag har vi placeret en celle til at drive STM -kortet. Der er også placeret to motorer på 4 volt på hver side med dæk tilsluttet, så robotten kan bevæge sig. I den øverste del af det første lag er der placeret to batterier på hver 4 volt (i alt 8 volt) og motordriver IC (L298N) til drift af motorer.

Andet lag

I det øverste lag af robotten har vi placeret STM Board på Perf Board. Endnu et perf bord med 4 optokoblere er placeret på det øverste lag. Gyroskop er også placeret på robotens øverste lag fra undersiden. Begge komponenter er placeret i den midterste del, så tyngdepunktet holdes så lavt som muligt.

Robotens tyngdepunkt

Tyngdepunktet holdes så lavt som muligt. Til dette formål har vi placeret tunge batterier på bundlaget og lette komponenter såsom STM -kort og optokoblere på det øverste lag.

Trin 7: Kode

Koden blev udarbejdet på Atollic TrueStudio. STM studio blev brugt til fejlfinding.

Trin 8: Konklusion

Efter meget eksperimentering og observation er vi endelig kommet til det punkt, hvor vi opsummerer vores resultater og diskuterer, hvor langt det lykkedes os at implementere og udarbejde systemets effektivitet.

Generel gennemgang

Under forsøget blev motorens hastighed kontrolleret med succes ved hjælp af PID -algoritmen. Kurven er dog ikke ligefrem en glat lige linje. Det er der mange grunde til:

• Sensoren, selvom den er tilsluttet et lavpasfilter, leverer stadig visse endelige afbrydelser; disse skyldes de ikke -lineære modstande og nogle uundgåelige årsager til den analoge elektronik.

• Motoren roterer ikke jævnt under lille spænding eller PWM. Det giver ryk, der kan forårsage nogle forkerte værdier, der tilføres systemet.

• På grund af vaklen kan sensoren savne nogle slidser, der giver højere værdier. • En anden væsentlig årsag til fejl kan være kerneklokkefrekvensen for STM -mikrokontrolleren. Denne model af STM mikrokontroller giver et kerneklok på 168MHz. Selvom dette problem blev behandlet i dette projekt, er der en overordnet forestilling om denne model om, at den ikke ligefrem giver så høj frekvens.

Open loop -hastigheden giver en meget jævn linje med kun få uventede værdier. PID -algoritmen fungerer også fint, hvilket giver en meget lav afregningstid for motoren. Motorens PID -algoritme blev testet under forskellige spændinger, der holdt referencehastigheden konstant. Spændingsændringen ændrer ikke motorens hastighed, hvilket viser, at PID -algoritmen fungerer fint

Effektivitet

Her diskuterer vi effektiviteten af PID -controlleren, som vi observerede under eksperimentet.

Enkel implementering

Vi har set i afsnittet eksperimentering og observationer, at en PID -controller er meget let at implementere. Det kræver kun tre parametre eller konstanter, der skal indstilles for at få et hastighedskontrolsystem

Uovertruffen effektivitet for lineære systemer

Lineær PID -controller er den mest effektive i familien af controllere, fordi logikken er meget enkel, og applikationen er udbredt i tilfælde af lineære eller ret lineære applikationer.

Begrænsninger

Vi forklarede abstrakt om systemets begrænsninger. Her diskuterer vi et par af dem, som vi observerede.

Udvælgelse af konstanter

Vi har set, at selvom en PID -controller er let at implementere, er det stadig en stor ulempe ved systemet, at trinnet med at vælge værdien af konstanter er en besværligt trin; som man skal lave vanskelige beregninger. Den anden måde er hit and trial metoden, men det er heller ikke effektivt.

Konstanter er ikke altid konstante

De eksperimentelle resultater viste, at for forskellige værdier af referencehastigheden for motoren fejlede PID -controlleren for de samme værdier for PID -konstanterne. For forskellige hastigheder skulle konstanterne vælges forskelligt, og dette øger beregningsomkostningerne eksponentielt.

Ikke lineær

PID -controlleren, der bruges i vores tilfælde, er lineær, derfor kan den kun anvendes på lineære systemer. For ikke-lineære systemer skal controlleren implementeres forskelligt. Selvom der findes forskellige ikke -lineære metoder til PID, kræver det, at flere parametre vælges. Dette gør igen systemet uønsket på grund af høje beregningsomkostninger.

Initial Push påkrævet

Vi viste i eksperimentafsnittet, at for en temmelig lille referencehastighed, hvor fejlen er ret lille i starten, er PWM leveret af PID så lille, at den ikke genererer det nødvendige startmoment for motoren. Så motoren i nogle forsøg kører ikke eller i andre forsøg giver et stort overskridelse og en længere afregningstid.

Trin 9: Særlig tak

Særlig tak til mine gruppemedlemmer, der hjalp mig igennem dette projekt.

Jeg vil snart uploade linket til videoen.

Jeg håber, at du finder dette instruerbart interessant.

Dette er Tahir Ul Haq fra UET, der underskriver. Skål !!!