Grid Tie Inverter: 10 trin (med billeder)

2024 Forfatter: John Day | [email protected]. Sidst ændret: 2024-01-30 08:26

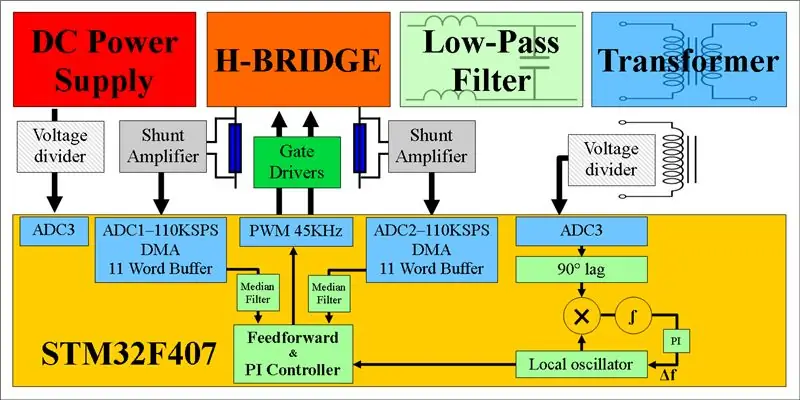
Dette er et kødfuldt projekt, så spænd op!

Inverter med netbinder gør det muligt at skubbe strømmen ind i en stikkontakt, hvilket er en fantastisk evne. Jeg synes, at magtelektronik og kontrolsystemer, der er involveret i deres design, er interessante, så jeg byggede mit eget. Denne rapport deler det, jeg lærte, og dokumenterer, hvordan jeg gjorde tingene. Jeg ville være interesseret i eventuelle kommentarer, du havde (bortset fra dem om ikke at rode med el).

Alle begreberne er skalerbare, men denne opsætning havde en maksimal effekt på 40 watt, før filterinduktorerne begyndte at mætte. Udgangsstrømmen var sinusformet med THD <5%.

Se softwaren på min GitHub

Forbrugsvarer

• Jeg brugte udviklingsbordet STM32F407. Den kører på 168MHz og har 3 indbyggede ADC'er, der er i stand til 12bit opløsning ved over 2,4MSPS (million prøver pr. Sekund) hver. Det er sindssygt!
• Jeg brugte udviklingsbrættet DRV8301. Dette huser en 60v H-bro sammen med de nødvendige portdrivere, nuværende shunts og nuværende shuntforstærkere. Super flot!
• Jeg brugte en 230-25v toroidformet transformer med 2 output haner. Dette betød, at jeg ikke behøvede at producere netspænding direkte, men kunne arbejde med spidsspændinger på 40 volt i stedet. Meget mere sikkert!
• Jeg forbandt en mængde induktorer og kondensatorer sammen for at få de L- og C -værdier, jeg ønskede for filteret.
• Et oscilloskop og differentialprobe er nøglen til et projekt som dette. Jeg har et Picoscope

Trin 1: Hvad er netstrøm?

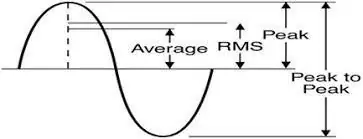
Hvad du får ved en stikkontakt (i Storbritannien) er et 50Hz 230v RMS sinusformet signal med en meget lav impedans. Et par ting at sige om det:

50Hz - Netfrekvensen opretholdes meget præcist ved 50Hz. Det varierer lidt, men 90% af tiden er det mellem 49,9-50,1Hz. Se her. Du kan forestille dig, at alle de enorme generatorer på kraftværker op og ned ad landet snurrer i fællesskab. De roterer synkront og producerer et 50Hz sinusformet signal for os. Deres kombinerede massive rotationsinerti tager tid at bremse eller fremskynde.

I teorien, hvis en KÆMPE belastning blev knyttet til nettet, ville det begynde at bremse landets generatorer. Som svar ville fyrene i National Grid's kontrolkontor bede kraftværker om at stikke deres kedler op, skrue op for varmen og tvinge disse generatorer sværere til at følge med efterspørgslen. Således er udbud og efterspørgsel i en kontinuerlig dans med hinanden.

En ting mere at sige om 50Hz -signalet. Selvom det varierer meget lidt omkring 50Hz, sørger fyrene i top for, at den gennemsnitlige frekvens i løbet af dagen er præcis 50Hz. Så hvis nettet er på 49,95Hz i 10 minutter, vil de sikre, at det kører på 50,05Hz senere for at bringe det nøjagtige antal cyklusser til 50Hz x 60sekunder x 60minutter x 24 timer = 4, 320, 000/dag. De gør dette præcist ved hjælp af International Atomic Time. Husholdnings-, kontor- og industriapparater kan derfor bruge netfrekvensen til at holde tiden. Dette gøres sædvanligvis f.eks. Med mekaniske fatningstimere.

230v - Dette er RMS (Root Mean Square) spændingen for 50Hz signalet. Det egentlige signal svinger op til en 325v top. Dette er vigtigt at vide, for hvis du bygger en inverter, skal du producere så høje spændinger, hvis du skal få strøm til at strømme ind i stikket.

I virkeligheden er spændingerne set ved et stik i dit hus ret varierende. Det skyldes spændingsfald over modstanden i ledninger, stik, sikringer, transformere osv. Der er modstand overalt. Hvis du tænder et elektrisk brusebad, der trækker 11 kilowatt (det er ~ 50Amps), vil selv 0,2 ohm modstand falde dig 10 volt. Du kan se dette som, at lysene dæmpes så lidt. Store motorer, såsom dem i hoover, trækker enorme strømme, mens motoren kommer op i fart. Så du ser ofte en lille flimmer af lysene, når du tænder dem.

Min pointe er, at netspændingen er meget mere variabel. Her i Storbritannien skal det være 230v med en +10%/-6% tolerance. Du kan forvente at se pludselige ændringer og udsving, når store belastninger i nærheden tænder/slukker. Tænk tørretumblere, elkedler, ovne, hoovers osv.

Sinusformet - Signalet skal være en fin ren sinusbølge, men i virkeligheden suger nogle ikke -lineære apparater deres strøm fra bestemte punkter i sinusbølgecyklussen. Dette introducerer forvrængning, og derfor er signalet ikke en perfekt sinusbølge. Ikke -lineære belastninger omfatter typisk computerens strømforsyninger, lysstofrør, opladere, fjernsyn osv.

Total harmonisk forvrængning (THD) kvantificerer dette i bølgeformen. Der er regler for, hvor ren en inverters output skal være. Hvis det ikke er i stand til at producere et rent nok signal, bliver det ikke godkendt til salg. Dette er vigtigt, fordi harmonisk indhold i nettet reducerer effektiviteten af nogle enheder, der er tilsluttet det (især ulige harmoniske). Jeg tror, at den maksimalt tilladte THD er 8%

Lav impedans - Når du tænker på en grid tie inverter, vil dette være vigtigt at overveje. Der er alle slags belastninger knyttet til lysnettet, herunder induktive, resistive og lejlighedsvis kapacitive belastninger. Så impedansen er ukendt og foranderlig. Modstanden er meget lille, hvilket betyder, at hvis du tilslutter en høj strømbelastning, vil spændingen slet ikke falde meget.

Trin 2: Sådan skubbes strømmen ind i nettet

For at skubbe strømmen ind i netværket skal vi syntetisere et signal, der nøjagtigt matcher frekvensen og fasen på lysnettet, men med en spænding, der er lidt højere.

På grund af netets lave modstand er det svært at vide præcis, hvor meget højere at lave denne spænding. Og da RMS -spændingen svinger, skal vi sikre, at vi svinger med den. Bare at producere et fast 50Hz spændingssignal lidt højere end netspændingen virker ikke!

PI Kontrol af udgangsstrømmen

Det, vi har brug for, er en kontrolsløjfe, hvorved vi måler den øjeblikkelige strøm, vi skubber ind i nettet, og justerer automatisk vores udgangsspænding for at drive den strøm, vi ønsker. Dette vil effektivt omdanne vores output til en strømkilde (snarere end en spændingskilde), som er mere passende til at drive lave impedanser. Vi kan opnå dette ved at bruge en PI (Proportional Integral) kontrol loop:

PI kontrol sløjfer er fantastiske! Der er 3 dele til dem:

• Den målte værdi - den strøm, vi sætter i lysnettet
• Setpunktet - Den strøm, vi ønsker at skubbe ind i lysnettet
• Output - Signalspændingen, der skal genereres

Hver gang vi kalder PID -algoritmen, passerer vi den seneste aktuelle måling og det setpunkt, vi ønsker. Det returnerer et vilkårligt tal (proportionalt med den udgangsspænding, der skal genereres).

Vores PID -kontrolalgoritme giver os mulighed for at vælge den udgangsstrøm, vi ønsker på et givet tidspunkt. For at producere en 50Hz sinusformet udgangsstrøm skal vi løbende ændre vores ønskede strøm på en sinusformet måde.

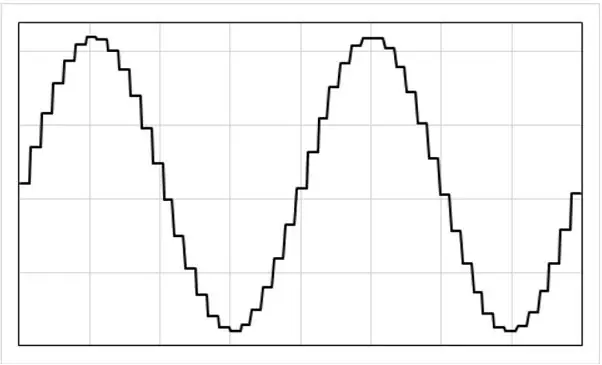
PID -algoritmen kaldes for hver 100us (svarende til 200 gange pr. 50Hz -cyklus). Hver gang det kaldes, er det i stand til at foretage direkte justeringer af udgangsspændingen og dermed indirekte justere udgangsstrømmen. Som et resultat producerer vi en trinvis strømudgang svarende til den, der er vist på billedet, hvor hvert trin forekommer for hver 100us. Det giver nok opløsning.

Feedforward -kontrol

Vi kan massivt reducere PI -controllerens arbejdsbyrde ved også at tilføje en feedforward -controller. Det er let! Vi kender den omtrentlige udgangsspænding, vi skal generere (samme som den øjeblikkelige netspænding). PI -controlleren kan derefter efterlades for at tilføje den lille ekstra spænding, der er nødvendig for at drive en udgangsstrøm.

I sig selv matcher feedforward -controlleren inverterens udgangsspænding til netets spænding. Ingen strøm bør flyde, hvis vi matcher godt nok. Feedforward -kontrollen udfører derfor 99% af outputstyringen.

På grund af netets lave modstand ville enhver forskel i vores FF -udgangsspænding og netspændingen resultere i en stor strøm. Jeg tilføjede derfor en 1ohm buffer modstand mellem inverteren og nettet. Dette medfører tab, men de er ret små i den store ordning.

Trin 3: Fremstilling af udgangsspændingen ved hjælp af PWM

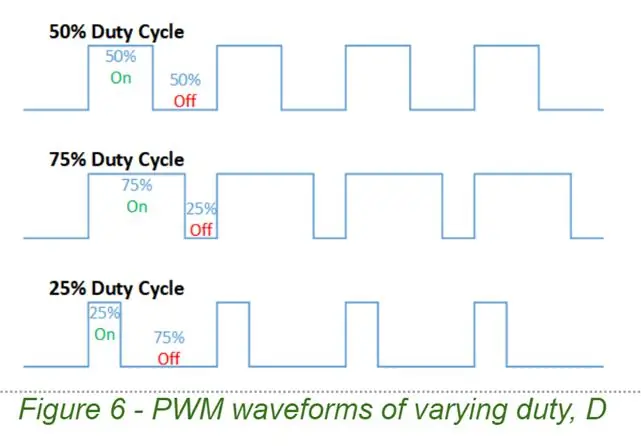
Selvom vi indirekte styrer udgangsstrømmen, er det en udgangsspænding, som vi genererer på et givet tidspunkt. Vi bruger PWM (Pulse Width Modulation) til at producere vores udgangsspænding. PWM-signaler kan let produceres af mikrokontrollere, og de kan forstærkes ved hjælp af en H-bro. De er enkle bølgeformer karakteriseret ved 2 parametre, frekvensen F og driftscyklus D.

En PWM -bølgeform skifter mellem 2 spændinger, i vores tilfælde 0v og Vsupply

• Med D = 1.0 er PWM -kurven simpelthen DC ved Vsupply
• Med D = 0,5 får vi en firkantbølge med en gennemsnitlig spænding på 0,5 x Vsforsyning, (dvs. D x Vsupply)
• Med D = 0,1 får vi en pulserende bølgeform med et periodegennemsnit på 0,1 x Vsforsyning
• Med D = 0,0 er udgangen en flad linje (DC ved 0v)

Den gennemsnitlige spænding er nøglen. Med et lavpasfilter kan vi fjerne alt andet end DC-gennemsnitskomponenten. Så ved at variere PWM -driftscyklussen D, er vi i stand til at lave enhver ønsket DC -spænding. Sød!

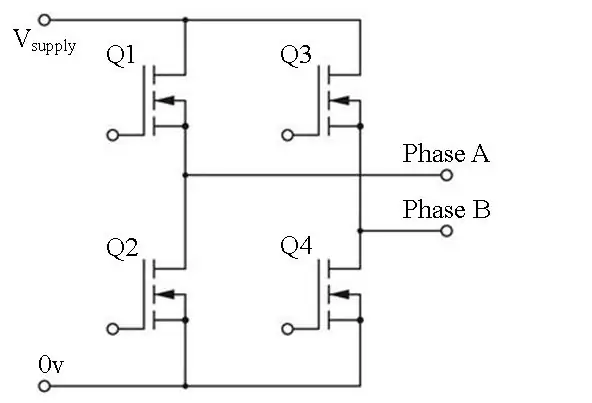
Ansættelse af en H-bro

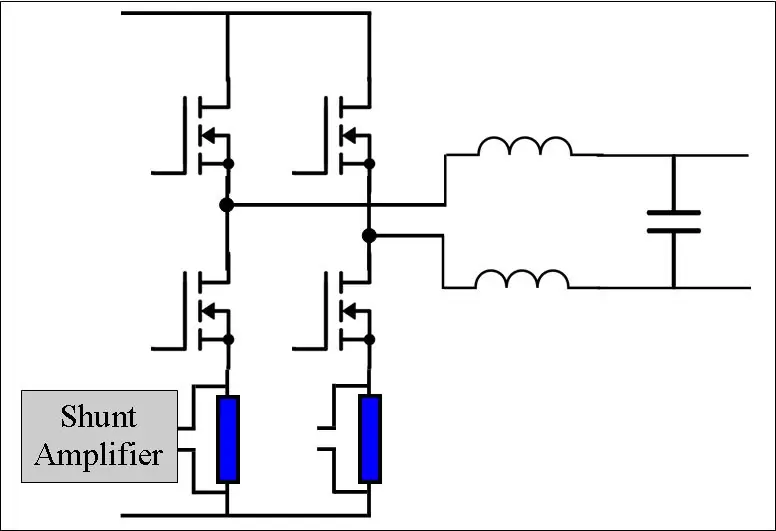
En H-bro består af 4 skifteelementer. Disse kan være BJT'er, MOSFET'er eller IGBT'er. For at producere den første halvdel (0 - 180 grader) af sinusbølgen, sætter vi fase B lav ved at slukke Q3 og Q4 (dvs. anvende PWM med D = 0). Vi udfører derefter vores PWMing på fase A. I anden halvdel, hvor VAB er negativ, sætter vi fase A lav og anvender vores PWM til fase B. Dette er kendt som bipolar switch.

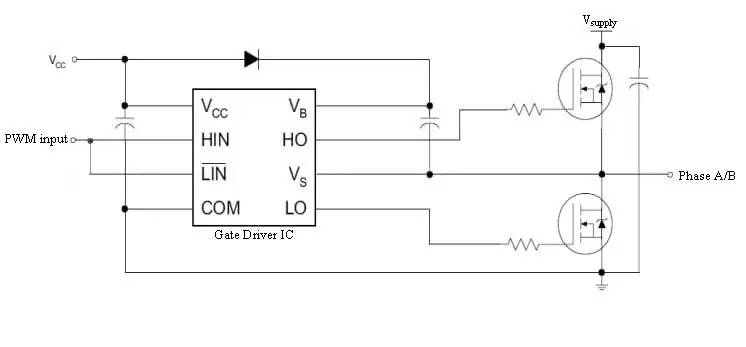
MOSFET'erne i H-broen skal drives af en portdriver. Dette er et eget emne, men en simpel chip kan tage sig af det. DRV8301 dev-pladen huser bekvemt H-broen, portdrivere og aktuelle shunts for os, hvilket gør dette projekt meget lettere.

Trin 4: Måling af strøm

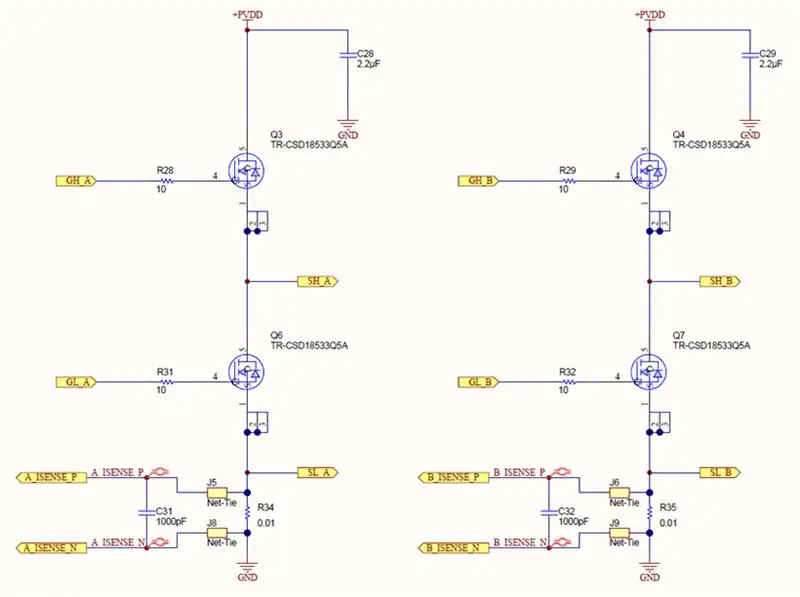
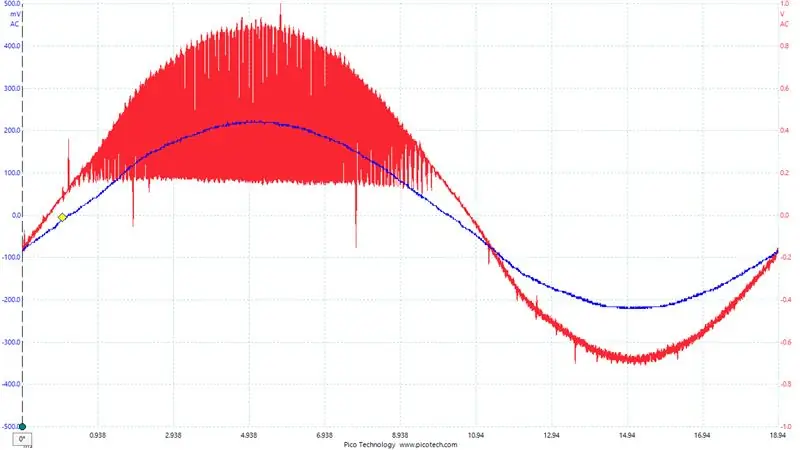
Hvert ben på H-broen har en shuntmodstand og en differentialforstærker. Vores shunts er 0,01 ohm, og vores forstærkere er indstillet til en forstærkning på 40. Derfor udvikler 1 Amp 10mV hen over shunten, som efterfølgende forstærkes til 400mV.

Outputene fra shuntforstærkerne læses af 12bit ADC'erne på STM32F407, der kører i kontinuerlig konverteringstilstand. ADC'erne er indstillet til at prøve hver shunt ved 110KSPS, og DMA -controlleren skriver automatisk konverteringerne til en cirkulær buffer på 11 ord i RAM. Når en aktuel måling ønskes, kalder vi en funktion, der returnerer medianværdien af denne 11 ords buffer.

Da vi anmoder om aktuelle målinger hver PID -iteration (ved 10KHz), men fylder vores 11 -ords ADC -buffere med en hastighed på 110KHz, bør vi få helt friske data for hver PID -iteration. Grunden til at bruge et medianfilter er, at PWM -switch kan introducere pigge i blandingen, og medianfiltre udrydder falske ADC -prøver meget effektivt.

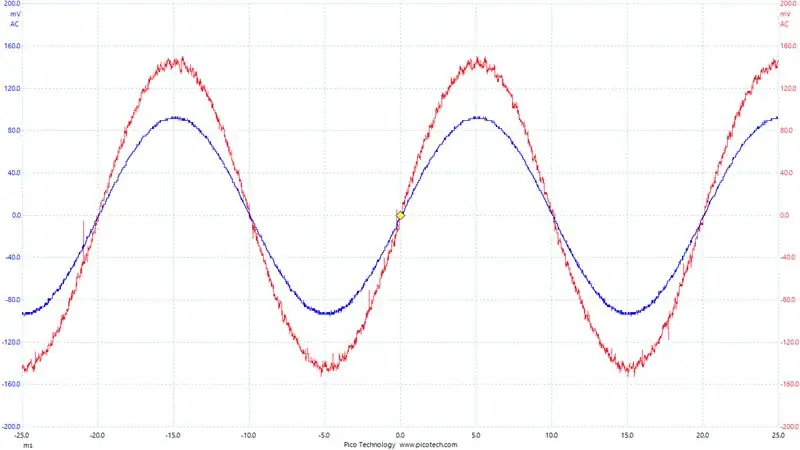
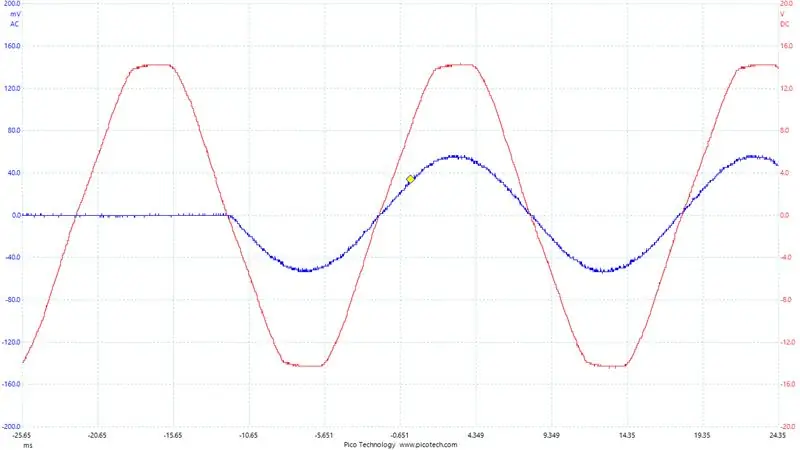
Et vigtigt punkt at gøre her: Hvilket ben af H-broen bruger vi til aktuelle målinger? Det afhænger godt af, hvilket ben vi i øjeblikket PWMing, og som bare holdes lavt. Benet holdt lavt er det, vi vil måle vores strøm ud fra, da strømmen altid flyder gennem shuntmodstanden på den side. Til sammenligning, på den side, der er PWMed, når MOSFET på høj side er tændt, og lavsiden er slukket, strømmer der ingen strøm gennem lavsideshunten. Så vi ændrer hvilket ben vi måler strøm på baseret på omformerens outputpolaritet. Du kan se dette tydeligt på billedet, der viser output fra en af shuntforstærkerne over en periode. Det er klart, at vi vil tage aflæsninger under den glatte bit.

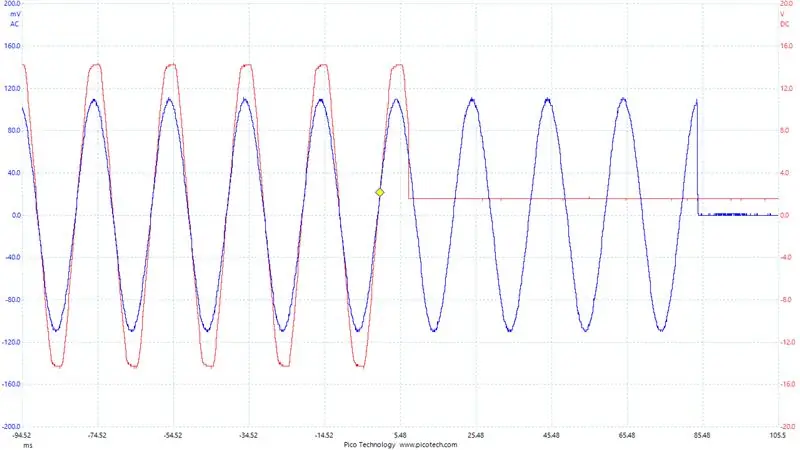
For at hjælpe med at fejlsøge vores nuværende aflæsninger. Jeg konfigurerede Digital-til-analog-konverteren på STM32F407. Jeg skrev de aktuelle aflæsninger, jeg fik, og omfattede output. Du kan se dette i det sidste billede, det blå er spændingen over outputbuffermodstanden (dvs. udgangsstrømmen/1,1 ohm) og det røde signal er vores DAC -udgang.

Trin 5: Filtrering af output

Outputfilteret er en vigtig del af designet. Vi har brug for disse egenskaber fra det:

1. Bloker alle højfrekvente skift, men send et 50Hz signal
2. Lavt tab
3. Ikke for at give genlyd!
4. For at klare de involverede strømme og spændinger

Fouriertransformationen af et PWM -signal med frekvens F, driftscyklus D, mellem 0 - Vsupply volt er: (D x Vsupply) + Sinusbølger ved grundfrekvensen F og harmoniske derefter

Dette er genialt! Det betyder, at hvis vi sætter vores PWM -signal gennem et lavpasfilter, der blokerer PWM -fundamentet og alt ovenfor. Vi er lige tilbage med DC -spændingsbetegnelsen. Ved at variere driftscyklussen kan vi let producere enhver spænding, vi ønsker mellem 0 - Vsforsyning som forklaret.

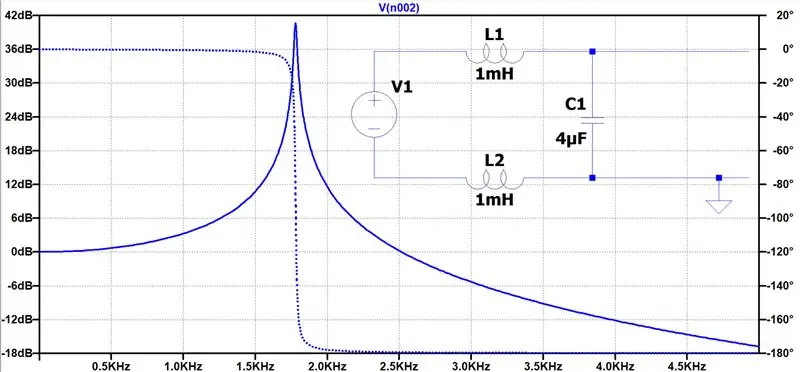
Baseret på de ønskede egenskaber nævnt ovenfor kan vi designe outputfilteret. Vi har brug for et lavpasfilter lavet med minimal modstand for at undgå tab. Derfor bruger vi bare induktorer og kondensatorer. Hvis vi vælger en resonansfrekvens mellem 1 - 2KHz, undgår vi resonans, da vi ikke injicerer nogen signaler nær denne frekvens. Her er vores filterdesign. Vi tager vores output som spændingen over C1.

Ved at vælge L1 = L2 = 440uH, C1 = 8.4uF beregner vi en resonansfrekvens på 1.85KHz. Det er også realistiske komponentværdier.

Det er vigtigt at sikre, at vores spoler ikke begynder at mætte ved de strømme, vi forventer. De induktorer, jeg har brugt, har en 3A mætningsstrøm. Dette vil være den begrænsende faktor for vores kredsløbs udgangseffekt. Kondensatorens spændingsværdi er også vigtig at overveje. Jeg bruger noget 450v keramik, hvilket er meget overkill i dette tilfælde!

Bode -plottet (for lidt forskellige L/C -værdier) er blevet genereret ved hjælp af LTspice. Det viser os den dæmpning, der påføres forskellige inputfrekvenser. Vi kan tydeligt se resonansfrekvensen ved 1,8KHz. Det viser, at et 50Hz signal er næsten helt uforfalsket, hvorimod jeg kan fortælle dig, at et 45 KHz signal er dæmpet med 54dB!

Så lad os vælge vores PWM -bærefrekvens til ~ 45KHz. Ved at vælge højere PWM -bærefrekvenser kan filterfrekvensen gøres højere. Det er godt, fordi det gør L- og C -værdierne mindre. Det betyder mindre og billigere komponenter. Bagsiden er, at højere PWM -skiftefrekvenser introducerer større tab i transistorkontakterne.

Trin 6: Synkronisering af fase og frekvens

Synkronisering med netfasen og frekvensen er det, der gør en grid tie inverter. Vi bruger en digital implementering af en PLL (Phase Locked Loop) for at opnå nøjagtig fasesporing af netsignalet. Vi gør dette ved at:

1. Prøveudtagning af netspændingen
2. Producerer et lokalt sinusformet signal på 50 Hz
3. Sammenligning af fasen mellem vores lokale signal og netsignalet
4. Justering af frekvensen af det lokale signal, indtil faseforskellen mellem de 2 signaler er nul

1) Prøveudtagning af netspændingen

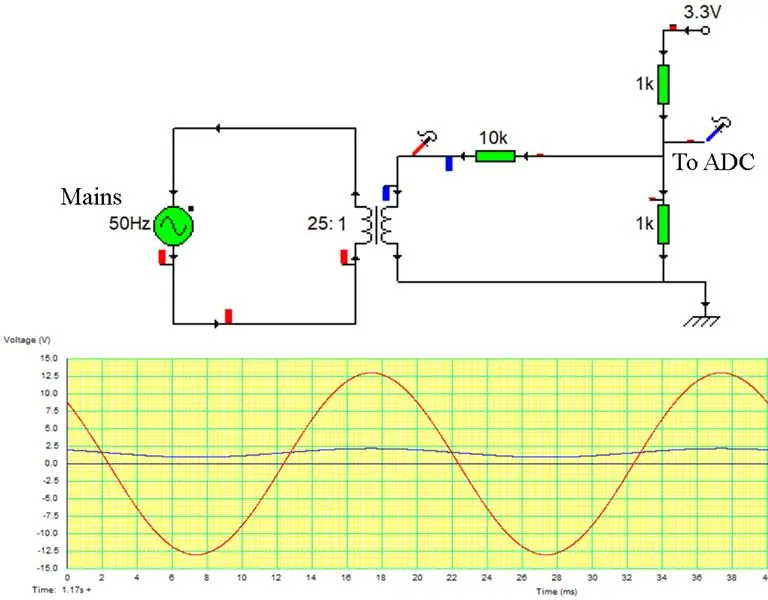
Vi konfigurerer en 3. ADC -kanal til at aflæse netspændingen. Dette får vi ved spændingsdeling af en transformerhane som vist. Dette giver en skaleret spænding, der varierer omkring 1,65v, der præcist repræsenterer netspændingen.

2) At producere et lokalt 50Hz sinusformet signal Det er let at producere vores egen lokale 50Hz sinusbølge. Vi gemmer en opslagstabel med 256 sinusværdier. Vores simulerede sinusværdi opnås let ved hjælp af et opslagsindeks, der roterer trinvist gennem tabellen.

Vi skal øge vores indeks med den helt rigtige hastighed for at få et 50Hz -signal. Nemlig 256 x 50Hz = 12, 800/s. Vi gør dette ved at bruge timer9, der er klokket til 168MHz. Ved at vente 168MHz/12800 = 13125 uret tikker vi trin vores indeks med den rigtige hastighed.

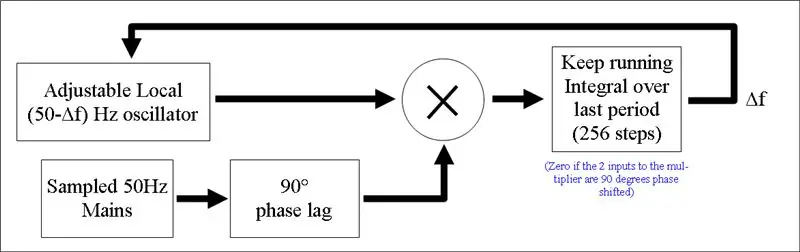
3) Sammenligning af fasen mellem vores lokale signal og netsignalet Dette er den fede del! Hvis du integrerer produktet af cos (vægt) x sin (vægt) over 1 periode, er resultatet nul. Hvis faseforskellen er andet end 90 grader, får du et nul -nummer. Matematisk:

Integral [Asin (t) x Bsin (t + φ)] = Ccos (φ)

Dette er godt! Det giver os mulighed for at sammenligne netsignalet, sin (ωt) med vores lokale signal, sin (⍵t + φ) og få en værdi.

Der er imidlertid et problem, der skal løses: Hvis vi vil have vores signaler til at forblive i fase, er vi nødt til at justere vores lokale frekvens for at holde Ccos (φ) udtrykket maksimalt. Dette fungerer ikke særlig godt, og vi får dårlig fasesporing. Dette skyldes, at d/dφ for ɑcos (φ) er 0 ved φ = 0. Dette betyder, at Ccos (φ) -udtrykket ikke vil variere særlig meget med ændringer i fase. Giver det mening?

Det ville være langt bedre at faseskifte det samplede netsignal med 90 grader, så det bliver cos (ωt + φ). Så har vi dette:

Integral [Asin (t) Bcos (t + φ)] = Csin (φ)

Det er let at indføre et 90 graders faseskift, vi sætter bare vores ADC -spændingsprøver i netspændingen ind i den ene ende af en buffer og tager dem ud et antal prøver senere, svarende til et faseskift på 90 grader. Da netfrekvensen næppe varierer fra 50Hz, fungerer en simpel tidsforsinkelsesteknik glimrende.

Vi multiplicerer nu vores 90 graders faseforskiftede netsignal med vores lokale signal og bevarer en løbende integral af produktet i løbet af den sidste periode (dvs. over de sidste 256 værdier).

Det resultat, vi ved, vil være nul, hvis de 2 signaler præcist holdes 90 grader fra hinanden. Dette er fantastisk, fordi det fortryder det faseforskydning, vi lige har anvendt på netsignalet. Bare for at præcisere, i stedet for at maksimere det integrerede udtryk, forsøger vi at holde det nul, og vi faseforskyder vores netsignal. De 90 graders faseforskydninger, der blev indført ved disse 2 ændringer, annullerer hinanden.

Så hvis Integral_Result <0 ved vi, at vi skal øge vores lokale oscillatorfrekvens for at bringe den tilbage i fase med elnettet, og omvendt.

4) Justering af frekvensen for det lokale signal Denne bit er let. Vi justerer simpelthen perioden mellem stigning gennem vores indeks. Vi begrænser, hvor hurtigt vi kan korrigere faseforskellen, der hovedsageligt filtrerer falske hvalpe ud. Vi gør dette ved hjælp af en PI -controller med et meget lille I -udtryk.

Og det er det. Vi har låst vores lokale sinusbølge -oscillator (som indstiller udgangsstrømens setpunkt) til at være i fase med netspændingen. Vi har implementeret en PLL -algoritme, og den fungerer som en drøm!

Forøgelse af frekvensen af vores lokale oscillator reducerer også faseforskydningen på netværkssignalet. Da vi begrænser frekvensjusteringen til +/- 131 kryds (+/- ~ 1%), påvirker vi faseskiftet højst med +/- 1 °. Dette får slet ingen betydning, mens faserne synkroniseres.

Teoretisk set, hvis netfrekvensen afviger med mere end 0,5 Hz, mister vi vores faselås. Dette er på grund af vores ovenstående begrænsning for, hvor meget vi kan justere vores lokale oscillatorfrekvens. Det kommer dog ikke til at ske, medmindre nettet er ved at mislykkes. Vores anti-ø-beskyttelse vil alligevel sparke ind på dette tidspunkt.

Vi udfører en nulkrydsningsdetektering ved opstart for at prøve vores bedste på at starte signalerne i fase fra offset.

Trin 7: Anti-islanding

Wikipedia har en fantastisk artikel, der handler om ø-teknik og anti-ø-teknik. Det indebærer også, at folk hvisler og klapper mere end nødvendigt, når det kommer til dette emne. "Åh, du kan ikke bygge din egen inverter til netbinder, du vil dræbe nogen osv. Osv."

Som forklaret bedre af wikipedia -artiklen anvender vi et par sikkerhedsforanstaltninger, der tilsammen giver tilstrækkelig beskyttelse (efter min mening):

1. Under-/overspænding
2. Under/Over frekvens

Vi kan opdage disse situationer ved blot at analysere vores samplede skalerede netspænding. Hvis noget går galt, skal du deaktivere H-broen og afvente, at tingene vender tilbage til det normale.