Eyeballing din Eyeball's recept: et BME60B -projekt: 9 trin

2024 Forfatter: John Day | [email protected]. Sidst ændret: 2024-01-30 08:25

Af: Hannah Silos, Sang Hee Kim, Thomas Vazquez, Patrick Viste

Forstørrelse er en af de vigtigste egenskaber, der er til stede for læsebriller, som er klassificeret efter deres recept på dioptrier. Ifølge Michigan Technology University er en diopter en brændvidde af linsen, normalt målt i mm, i måleenheden (Michigan Technology University). Fordi læsebriller har konvekse linser, ville brændvidden være positiv, hvilket også får dioptrierne til at være positive (HyperPhysics). Brændvidden øges, efterhånden som afstanden mellem objektet kommer længere væk fra den faktiske linse, og dette får dioptrierne til at falde, da de er omvendt proportionale. Derfor ville have læsebriller med ekstra dioptrier hjælpe linsen med at zoome ind i visningen, så det kan virke som om brændvidden er mindre ved at øge værdien af dioptrierne.

Den præsenterede kode vil blive brugt til at forudsige dioptrien af en linse med en ukendt recept. To input bruges til at beregne recepten: et fotografi af den kontrollerede baggrund uden brug af linser, og et andet fotografi med samme baggrund, men gennem den valgte linse. Programmet måler forvrængningen mellem disse to fotografier. Derfra vil vi kunne estimere objektivets dioptri og producere et resultat, som brugeren kan se.

Til denne instruktive skal du bruge:

• Et sort-hvidt tavlemønster trykt på et 11x8,5 i ark papir
• Et kamera med mulighed for at låse sit fokus
• Et stativ eller lignende for at sikre kameraet
• Forskellige forskrifter på læsebriller
• MATLAB

Trin 1: Tag fotos

For at beregne forstørrelsen af et objektiv, skal du kunne sammenligne det med objektets faktiske størrelse. For dette projekt vil vi sammenligne et forstørret billede med et kontrolbillede.

Således er det første trin at tage to fotos af det samme billede - det første gennem bare kameraet, og det andet gennem linsen på de læsebriller, du vil teste.

Du tager et billede af et 8.5x11in sort og hvidt skakbræt med et 1in -gitter. Sæt dit kamera 11in væk fra skakbrættet. Inden du tager billederne, skal du låse fokus på skakbrættet.

Tag et foto af skakbrættet uden læsebrillerne. Placer derefter læsebrillen foran kameraet uden at flytte noget, og tag det andet foto.

Sørg for, at kameraets position ikke bevæger sig mellem optagelserne. Det eneste, der bør ændre sig mellem de to fotos, er tilstedeværelsen af brilleglasset foran kameraet.

Når du er færdig med billederne, skal du uploade dem til din computer.

Trin 2: Indlæs billederne i MATLAB

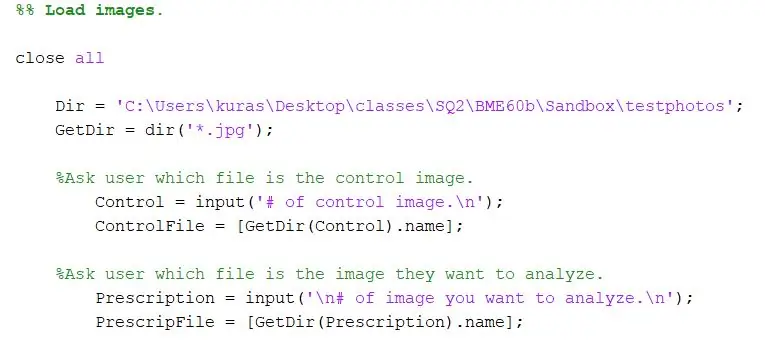
Åbn et nyt script.

Angiv først det bibliotek, hvor fotos skal gemmes. Brug derefter dir -funktionen til at udtrække-j.webp

Dir = 'C: / Users / kuras / Desktop / classes / SQ2 / BME60b / Sandbox / testphotos'; GetDir = dir ('*. Jpg');

Til vores projekt ønskede vi at bede brugeren af programmet om, hvilke filer de ville sammenligne. Det første afsnit beder brugeren om at angive kontrolbilledet, og det andet beder brugeren om at angive testbilledet.

• %Spørg brugeren, hvilken fil der er kontrolbilledet.
• Kontrol = input ('# af kontrolbillede. / N');
• ControlFile = [GetDir (Control).navn]
• %Spørg brugeren, hvilken fil er det billede, de vil analysere.
• ChooseFile = input ('\ n# af billede, du vil analysere. / N');
• PrescripFile = [GetDir (ChooseFile).navn];

Trin 3: Billedanalyse

Et farvet billede i MATLAB er af størrelse MxNx3, hvorimod et gråtonebillede er MxN. Det betyder, at det er hurtigere at forbedre/redigere et gråtonebillede, fordi der er færre data at holde styr på. Brug rgb2gray til at konvertere billedet til gråtoner. (Imrotateringsfunktionen blev brugt, fordi vores fotos stod vandret - denne kodelinje er muligvis ikke nødvendig i din version.)

• %konverter til gråtoner og drej
• I = imread (ControlFile);
• I = rgb2gray (I);
• I = imrotate (I, 90);

Vis derefter billedet. Subplot -funktionen bruges, så testbilledet vil kunne være ved siden af kontrolelementet i senere trin.

• %Skærm
• figur 1);
• delplot (1, 2, 1)
• imshow (I);
• titel (ControlFile);

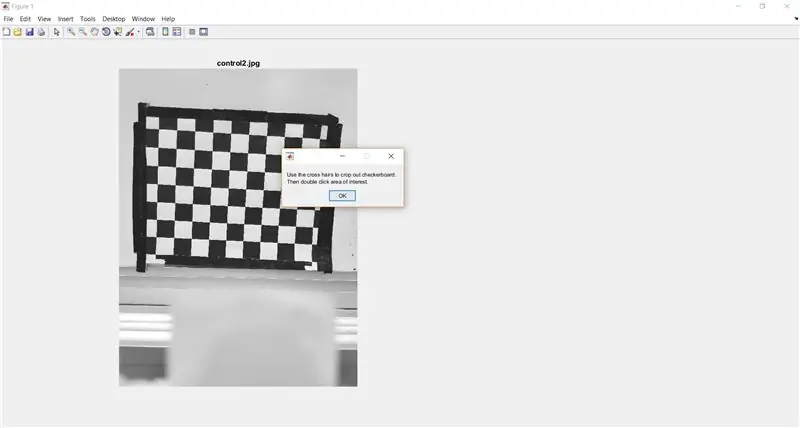
Brug imcrop til at bede brugeren om at beskære tavlen ud af det fulde billede. Følgende kode viser også en meddelelsesboks for at give brugeren instruktioner.

• %beskære skakbræt til analyse
• waitfor (msgbox ({'Brug krydshårene til at beskære tern.', 'Dobbeltklik derefter på interesseområde.'}));
• I_crop = imcrop (I);

Brug imbinarize til at binære billedet.

I_binary = imbinarize (I_crop);

Trin 4: Beregn bredden af de hvide firkanter på skakbrættet

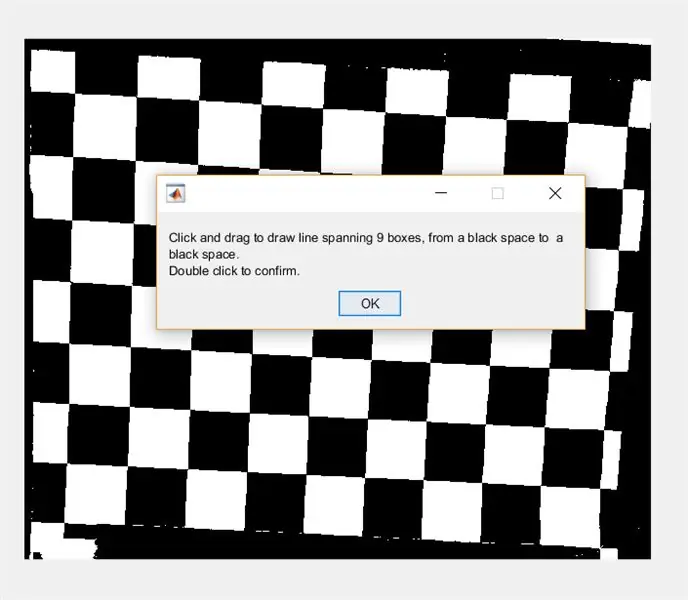
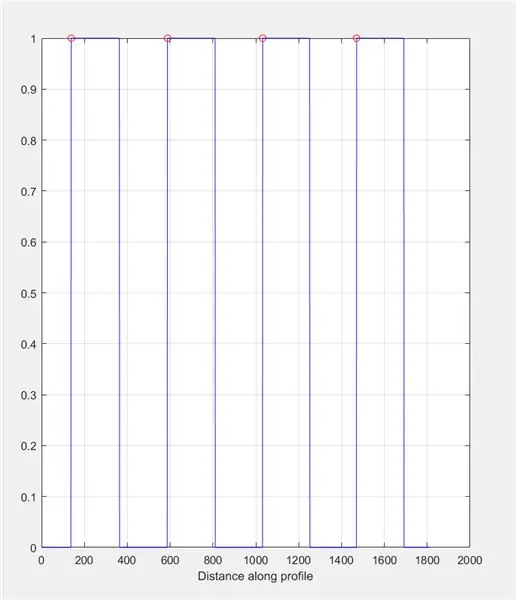
Bed derefter brugeren om at tegne en streg over billedet ved hjælp af imline. Denne linje skal løbe vandret hen over skakbrættet. Det skal starte og slutte på en sort firkant (det er ligegyldigt hvor)- det er fordi vi måler bredden af de hvide firkanter, ikke de sorte.

• %tegne streg
• figur 1)
• delplot (1, 2, 1)
• imshow (I_binary);
• waitfor (msgbox ({'Klik og træk for at tegne linje, der spænder over 9 bokse, fra et sort mellemrum til et sort mellemrum.', 'Dobbeltklik for at bekræfte.'}));
• linje = imline;
• position = vent (linje);
• endepunkter = line.getPosition;

Udtræk X- og Y -koodinaterne for slutpunkterne for den tegnede linje.

• X = endepunkter (:, 1)
• Y = endepunkter (:, 2);

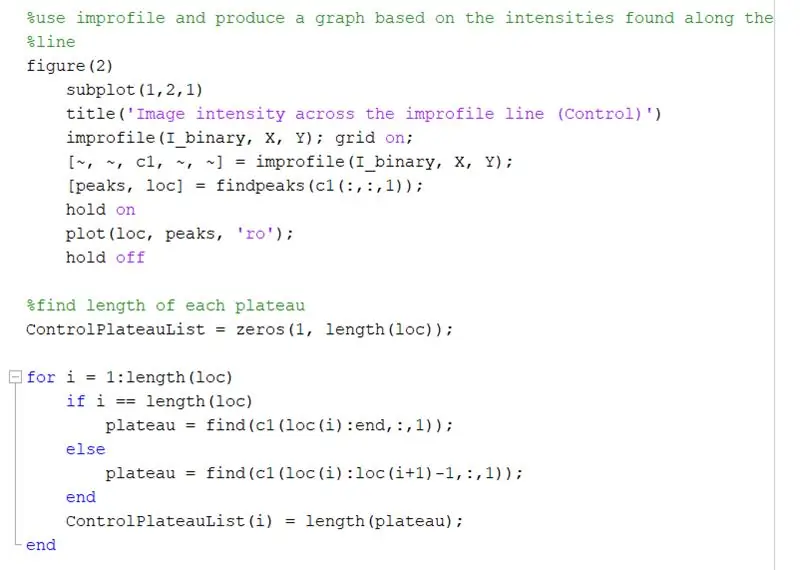
Brug improfil til at producere en graf baseret på intensiteterne fundet langs den tegnede linje. Dette skal ligne en firkantbølge, der spænder fra 0 (sort) til 1 (hvid). Beregn også toppene og deres placering.

• figur (2)
• delplot (1, 2, 1)
• titel ('Billedintensitet på tværs af den uprofilerede linje (kontrol)')
• improfile (I_binary, X, Y); gitter på;
• [~, ~, c1, ~, ~] = improfile (I_binary, X, Y);
• [toppe, loc] = findpeaks (c1 (:,:, 1));
• hold fast
• plot (loc, toppe, 'ro');
• hold ud

Find længden af hvert plateau på den improfile graf ved hjælp af en for loop. Kør for -loop for den samme mængde toppe, der er i den improfile graf. For at beregne længden af hvert plateau skal du bruge 'find' -funktionen til at finde alle de steder, hvor der er en' 1 'i stedet for en' 0 'intensitetsværdi. Beregn derefter længden af denne matrix for at få plateauets samlede længde, som skal svare til bredden af en hvid firkant i pixels. ControlPlateauList = nuller (1, længde (loc));

for i = 1: længde (loc)

hvis i == længde (loc)

plateau = find (c1 (loc (i): ende,:, 1));

andet

plateau = find (c1 (loc (i): loc (i+1) -1,:, 1));

ende

ControlPlateauList (i) = længde (plateau);

ende

Trin 5: Gentag trin 3 og 4 for testbilledet

*Bemærk: Når du tegner den uprofilerede linje på testbilledet, skal du sørge for at tegne den på tværs af firkanterne, der svarer til den linje, du tegnede på kontrolbilledet.

Trin 6: Beregn forstørrelsen af objektivet

De forstørrede målinger beregnes ved at dividere middelværdien af plateauets længde, som blev beregnet i trin 5, med middelværdien af længden af kontrolplateauet, som blev beregnet i trin 4. Dette beregnes til at være 1.0884.

forstørrelse = middelværdi (plateauList)/middelværdi (ControlPlateauList);

Trin 7: Find R-kvadrat og brugerens recept via interpolation

Brug af koden:

• md1 = fitlm (GivenPrescription, MagArray);
• Rsquared = md1. Rsquared. Ordinary;

Vi kan finde R-kvadratværdien af grafen GivenPresciption (vores linsers givne værdier) versus MagArray (en matrix af forstørrelsesmålingerne, vi har beregnet tidligere). Ved at have en høj nok R-kvadratværdi kan det udledes, at der er en stærk nok korrelation til at retfærdiggøre brugen af denne metode. For dette særlige tilfælde var R-kvadratværdien 0,9912, hvilket tyder på en stærk korrelation og derfor er begrundet i at bruge denne metode i analyse.

Brug af funktionen:

Prescription = interp1 (MagArray, GivenPrescription, forstørrelse, 'lineær');

Vi kan interpolere den tilsvarende receptværdi (på x-aksen) i vores forstørrelsesforhold (en værdi på y-aksen) og finde, hvad brugerens recept er.

Interpolering af data er vigtig for, at denne metode fungerer, da den giver os mulighed for at antage oplysninger, vi ikke har, baseret på de oplysninger, vi har. Selvom en linje med bedst pasning teknisk set ville være en stærkere kandidat til denne antagelse, skaber grænser for at reducere antallet af output den samme effekt, som receptpligtige briller alligevel kommer i trinvise ensartede værdier. Dette forklares i senere trin.

Trin 8: Viser brugerens recept på en graf

Brug af følgende kode:

• figur;
• plot (GivenPrescription, MagArray, '-g')
• hold fast
• plot (recept, forstørrelse, 'bp')
• hold ud
• gitter
• legend ('Data', 'Interpolated Points', 'Location', 'NW')

Vi kan plotte en graf, der viser forstørrelsesforholdene versus den givne recept med en grøn linje og de fundne data for vores beregnede forstørrelse versus vores interpolerede recept med en blå stjerne. Derefter mærker forklaringen titlen, x-aksen og y-aksen og placerer forklaringen i øverste venstre hjørne.

Trin 9: Begræns din recept

Følgende kode bruges til at producere afrundingen til receptet:

• hvis recept <= 1.125

  CalculatedPrescription = '1.0';

• elseif Recept <= 1.375

  CalculatedPrescription = '1,25';

• elseif Recept <= 1.625

  CalculatedPrescription = '1,5';

• elseif Recept <= 1.875

  CalculatedPrescription = '1,75';

• elseif Recept <= 2,25

  CalculatedPrescription = '2.0';

• elseif Recept <= 2.625

  CalculatedPrescription = '2.5';

• elseif Recept <= 3

  CalculatedPrescription = '2,75';

• elseif Recept <= 3.375

  CalculatedPrescription = '3,25';

• andet

  CalculatedPrescription = 'ukendt';

• ende

Receptet fundet gennem interpolation afspejler ikke nødvendigvis den faktiske recept - det skyldes, at der altid vil være små variationer i analysen af fotoet på grund af menneskelige fejl. Således har vi brug for dette trin for at klassificere den faktiske recept.

De recepter, der gives, starter normalt fra 1,0 dioptrier og stiger med.25 i deres recepter, så efter beregning af recepten vil vi bestemme den recept, der bedst passer til det, brugeren muligvis har brug for. Efter beregning af recept, kører vi den gennem de givne If -sætninger for at kontrollere dens værdi og afgøre, hvilken recept der er nødvendig. Noget mindre end eller lig med 1.125, så er recepten 1.0. Noget mindre end eller lig med 1.375, recepten er 1.25. Noget mindre end eller lig med 1.625, er recepten 1.5. Noget mindre end eller lig med 1.845, recepten er 1.75. Og så videre.

Vi har værdierne stigende, da vi kontrollerer, om værdierne er mindre end. Hvis vi lavede værdierne, faldt den første if -sætning hele tiden med den første if -sætning. Hvis recept er den mindste, ønsker vi, at den genkender den som den mindste med det samme, så derfor er den mindste værdi, hvad vi startede med. Alt højere end den højeste værdi betyder, at recepten ikke er inden for rækkevidde med vores data, så det vil give "Ukendt" strenglæsning.