Indholdsfortegnelse:
- Trin 1: Installation af biblioteket
- Trin 2: Fourier Transform og FFT -koncepter
- Trin 3: Simulering af et signal
- Trin 4: Analyse af et simuleret signal - kodning
- Trin 5: Analyse af et simuleret signal - Resultater
- Trin 6: Analyse af et ægte signal - Tilslutning af ADC
- Trin 7: Analyse af et reelt signal - kodning
- Trin 8: Analyse af et reelt signal - Resultater
- Trin 9: Hvad med et afklippet sinusformet signal?

Video: 1024 prøver FFT -spektrumanalysator ved hjælp af en Atmega1284: 9 trin

2024 Forfatter: John Day | [email protected]. Sidst ændret: 2024-01-30 08:26


Denne relativt lette vejledning (i betragtning af kompleksiteten af dette emne) viser dig, hvordan du kan lave en meget enkel 1024 prøver spektrumanalysator ved hjælp af et Arduino -typekort (1284 smal) og seriel plotter. Enhver form for Arduino -kompatibelt bord vil klare, men jo mere RAM det har, den bedste frekvensopløsning får du. Det skal bruge mere end 8 KB RAM for at beregne FFT med 1024 prøver.
Spektrumanalyse bruges til at bestemme hovedfrekvenskomponenterne i et signal. Mange lyde (som dem, der frembringes af et musikinstrument) er sammensat af en grundfrekvens og nogle harmoniske, der har en frekvens, der er et helt tal af grundfrekvensen. Spektrumanalysatoren viser dig alle disse spektrale komponenter.
Du vil måske bruge denne opsætning som en frekvensmåler eller for at kontrollere enhver form for signaler, som du har mistanke om, at de bringer støj i dit elektroniske kredsløb.
Vi vil her fokusere på softwaredelen. Hvis du gerne vil lave et permanent kredsløb til en bestemt applikation, skal du forstærke og filtrere signalet. Denne prækonditionering er helt afhængig af det signal, du vil studere, afhængigt af dets amplitude, impedans, maksimale frekvens osv. … Du kan tjekke
Trin 1: Installation af biblioteket
Vi vil bruge ArduinoFFT -biblioteket skrevet af Enrique Condes. Da vi ønsker at spare RAM så meget som muligt, vil vi bruge udviklingsgrenen af dette lager, der gør det muligt at bruge float -datatypen (i stedet for dobbelt) til at gemme de samplede og beregnede data. Så vi skal installere det manuelt. Bare rolig, bare download arkivet og afpak det i din Arduino biblioteksmappe (f.eks. På Windows 10 standardkonfiguration: C: / Brugere / _din_brugernavn_ / Dokumenter / Arduino / biblioteker)
Du kan kontrollere, at biblioteket er korrekt installeret ved at kompilere et af de angivne eksempler, f.eks. "FFT_01.ino."
Trin 2: Fourier Transform og FFT -koncepter
Advarsel: Hvis du ikke kan tåle at se nogen matematisk notation, kan du springe til trin 3. Hvis du ikke får det hele, skal du overveje konklusionen i slutningen af afsnittet.
Frekvensspektret opnås via en Fast Fourier Transform -algoritme. FFT er en digital implementering, der tilnærmer det matematiske koncept for Fourier Transform. Under dette koncept når du får udviklingen af et signal efter en tidsakse, kan du kende dets repræsentation i et frekvensdomæne, sammensat af komplekse (virkelige + imaginære) værdier. Konceptet er gensidigt, så når du kender frekvensdomænerepræsentationen, kan du transformere det tilbage til tidsdomænet og få signalet tilbage præcis som før transformationen.
Men hvad skal vi gøre med dette sæt af beregnede komplekse værdier i tidsdomænet? Det meste vil blive overladt til ingeniører. For os vil vi kalde en anden algoritme, der vil transformere disse komplekse værdier til spektraldensitetsdata: det er en størrelse (= intensitet) værdi, der er knyttet til hvert frekvensbånd. Antallet af frekvensbånd vil være det samme som antallet af prøver.
Du kender bestemt til equalizer -konceptet, som dette Tilbage til 1980'erne Med den grafiske EQ. Nå, vi vil opnå den samme slags resultater, men med 1024 bånd i stedet for 16 og meget mere intensitetsopløsning. Når equalizeren giver et globalt syn på musikken, giver den fine spektralanalyse mulighed for præcist at beregne intensiteten af hvert af de 1024 bånd.
Et perfekt koncept, men:
- Da FFT er en digitaliseret version af Fourier -transformen, tilnærmer den sig det digitale signal og mister nogle oplysninger. Så strengt taget ville resultatet af FFT'en, hvis den blev transformeret tilbage med en omvendt FFT -algoritme, ikke give nøjagtigt det originale signal.
- Teorien overvejer også et signal, der ikke er begrænset, men det er et konstant varigt signal. Da vi kun vil digitalisere det i et bestemt tidsrum (dvs. prøver), vil der blive introduceret nogle flere fejl.
-
Endelig vil opløsningen af den analoge til digitale konvertering påvirke kvaliteten af de beregnede værdier.
I praksis
1) Samplingsfrekvens (noteret fs)
Vi vil prøve et signal, dvs. måle dets amplitude, hvert 1/fs sekund. fs er samplingsfrekvensen. For eksempel, hvis vi prøver ved 8 KHz, vil ADC (analog til digital konverter), der er ombord på chippen, levere en måling hvert 1/8000 sekund.
2) Antallet af prøver (noteret N eller prøver i koden)
Da vi skal hente alle værdierne, før vi kører FFT, bliver vi nødt til at gemme dem, og derfor vil vi begrænse antallet af prøver. FFT -algoritmen har brug for et antal prøver, der er en effekt på 2. Jo flere prøver vi har, jo bedre er det, men det kræver meget hukommelse, desto mere skal vi også gemme de transformerede data, der er komplekse værdier. Arduino FFT -biblioteket sparer lidt plads ved at bruge
- Et array med navnet "vReal" til at gemme de samplede data og derefter den reelle del af de transformerede data
- Et array kaldet "vImag" til at gemme den imaginære del af de transformerede data
Den nødvendige mængde RAM svarer til 2 (arrays) * 32 (bits) * N (samples).
Så i vores Atmega1284, der har en dejlig 16 KB RAM, gemmer vi maksimalt N = 16000*8 /64 = 2000 værdier. Da antallet af værdier skal være en effekt på 2, gemmer vi maksimalt 1024 værdier.
3) Frekvensopløsningen
FFT beregner værdier for lige så mange frekvensbånd som antallet af prøver. Disse bånd spænder fra 0 HZ til samplingsfrekvensen (fs). Derfor er frekvensopløsningen:
Fresolution = fs / N
Opløsningen er bedre, når den er lavere. Så for bedre opløsning (lavere) ønsker vi:
- flere prøver, og/eller
- en lavere fs
Men…
4) Minimal fs
Da vi vil se mange frekvenser, hvor nogle af dem er meget højere end den "grundfrekvens", kan vi ikke indstille fs for lavt. Faktisk er der Nyquist – Shannon sampling sætning, der tvinger os til at have en samplingsfrekvens langt over det dobbelte af den maksimale frekvens, vi gerne vil teste.
For eksempel, hvis vi gerne vil analysere alt spektret fra 0 Hz for at sige 15 KHz, hvilket er omtrent den maksimale frekvens, de fleste mennesker kan høre tydeligt, skal vi indstille samplingsfrekvensen til 30 KHz. Faktisk sætter elektronikere det ofte til 2,5 (eller endda 2,52) * maksimumsfrekvensen. I dette eksempel ville det være 2,5 * 15 KHz = 37,5 KHz. Almindelige samplingsfrekvenser i professionel lyd er 44,1 KHz (lyd -cd -optagelse), 48 KHz og mere.
Konklusion:
Punkt 1 til 4 fører til: Vi ønsker at bruge så mange prøver som muligt. I vores tilfælde med en 16 KB RAM -enhed vil vi overveje 1024 prøver. Vi vil prøve med den laveste samplingsfrekvens som muligt, så længe den er høj nok til at analysere den højeste frekvens, vi forventer i vores signal (mindst 2,5 * denne frekvens).
Trin 3: Simulering af et signal

I vores første forsøg vil vi lidt ændre TFT_01.ino -eksemplet givet i biblioteket for at analysere et signal bestående af
- Grundfrekvensen, indstillet til 440 Hz (musikalsk A)
- 3. harmonisk med halv kraft af det grundlæggende ("-3 dB")
- 5. harmonisk ved 1/4 af kraften i det grundlæggende ("-6 dB)
Du kan se på billedet over det resulterende signal. Det ligner virkelig meget et ægte signal, man nogle gange kan se på et oscilloskop (jeg vil kalde det "Batman") i situationer, når der er en klipning af et sinusformet signal.
Trin 4: Analyse af et simuleret signal - kodning
0) Inkluder biblioteket
#include "arduinoFFT.h"
1) Definitioner
I deklarationsafsnittene har vi
const byte adcPin = 0; // A0
const uint16_t prøver = 1024; // Denne værdi SKAL ALTID være en effekt på 2 const uint16_t samplingFrequency = 8000; // Vil påvirke timer maks. Værdi i timer_setup () SYSCLOCK/8/samplingFrekvens skal være et heltal
Da signalet har en 5. harmoniske (frekvens for denne harmoniske = 5 * 440 = 2200 Hz) skal vi indstille samplingsfrekvensen over 2,5 * 2200 = 5500 Hz. Her valgte jeg 8000 Hz.
Vi erklærer også de arrays, hvor vi vil gemme rådata og beregnet data
float vReal [prøver];
float vImag [prøver];
2) Instantiering
Vi opretter et ArduinoFFT -objekt. Dev -versionen af ArduinoFFT bruger en skabelon, så vi kan bruge enten float eller den dobbelte datatype. Float (32 bit) er nok i forhold til den overordnede præcision af vores program.
ArduinoFFT FFT = ArduinoFFT (vReal, vImag, samples, samplingFrequency);
3) Simulering af signalet ved at udfylde vReal -arrayet i stedet for at få det udfyldt med ADC -værdier.
I begyndelsen af Loop udfylder vi vReal -arrayet med:
float cycles = (((samples) * signalFrequency) / samplingFrequency); // Antal signalcyklusser, som samplingen vil læse
for (uint16_t i = 0; i <samples; i ++) {vReal = float ((amplitude * (sin ((i * (TWO_PI * cycles)) / samples))))) / / Byg data med positive og negative værdier */ vReal += float ((amplitude * (sin ((3 * i * (TWO_PI * cyklusser))/ prøver)))/ 2.0);/ * Byg data med positive og negative værdier */ vReal += float ((amplitude * (sin ((5 * i * (TWO_PI * cycles)) / samples))) / 4.0); / * Byg data med positive og negative værdier * / vImag = 0.0; // Den imaginære del skal nulstilles i tilfælde af looping for at undgå forkerte beregninger og overløb}
Vi tilføjer en digitalisering af grundbølgen og de to harmoniske med mindre amplitude. End vi initialiserer det imaginære array med nuller. Da dette array er udfyldt af FFT -algoritmen, skal vi rydde det igen før hver ny beregning.
4) FFT computing
Derefter beregner vi FFT og spektraltætheden
FFT.windowing (FFTWindow:: Hamming, FFTDirection:: Forward);
FFT.compute (FFTDirection:: Frem); / * Compute FFT */ FFT.complexToMagnitude (); / * Beregn størrelser */
FFT.windowing (…) operation ændrer rådataene, fordi vi kører FFT på et begrænset antal prøver. De første og sidste prøver viser en diskontinuitet (der er "ingenting" på den ene side). Dette er en fejlkilde. "Windowing" -operationen har en tendens til at reducere denne fejl.
FFT.compute (…) med retningen "Frem" beregner transformationen fra tidsdomænet til frekvensdomænet.
Derefter beregner vi størrelsesværdierne (dvs. intensiteten) for hvert af frekvensbåndene. VReal -arrayet er nu fyldt med størrelsesværdier.
5) Seriel plotter tegning
Lad os udskrive værdierne på den serielle plotter ved at kalde funktionen printVector (…)
PrintVector (vReal, (prøver >> 1), SCL_FREQUENCY);
Dette er en generisk funktion, der gør det muligt at udskrive data med en tidsakse eller en frekvensakse.
Vi udskriver også frekvensen af det bånd, der har den højeste størrelsesværdi
float x = FFT.majorPeak ();
Serial.print ("f0 ="); Serial.print (x, 6); Serial.println ("Hz");
Trin 5: Analyse af et simuleret signal - Resultater

Vi ser 3 pigge svarende til grundfrekvensen (f0), den 3. og 5. harmoniske, med halvdelen og 1/4 af f0 -størrelsen, som forventet. Vi kan læse øverst i vinduet f0 = 440.430114 Hz. Denne værdi er ikke ligefrem 440 Hz på grund af alle de ovenfor forklarede årsager, men den er meget tæt på den reelle værdi. Det var egentlig ikke nødvendigt at vise så mange ubetydelige decimaler.
Trin 6: Analyse af et ægte signal - Tilslutning af ADC

Da vi ved, hvordan vi skal gå frem i teorien, vil vi gerne analysere et reelt signal.
Ledningerne er meget enkle. Tilslut grunde sammen og signallinjen til A0 -stiften på dit kort gennem en seriemodstand med en værdi på 1 KOhm til 10 KOhm.
Denne seriemodstand beskytter den analoge indgang og undgår at ringe. Det skal være så højt som muligt for at undgå at ringe og så lavt som muligt for at levere nok strøm til at oplade ADC'en hurtigt. Se MCU -databladet for at kende den forventede impedans af det signal, der er tilsluttet ADC -indgangen.
Til denne demo brugte jeg en funktionsgenerator til at fodre et sinusformet signal med frekvens 440 Hz og amplitude omkring 5 volt (det er bedst, hvis amplituden er mellem 3 og 5 volt, så ADC'en bruges nær fuld skala), gennem en 1,2 KOhm modstand.
Trin 7: Analyse af et reelt signal - kodning
0) Inkluder biblioteket
#include "arduinoFFT.h"
1) Erklæringer og instanciering
I deklarationsafsnittet definerer vi ADC -input (A0), antallet af prøver og samplingsfrekvensen, som i det foregående eksempel.
const byte adcPin = 0; // A0
const uint16_t prøver = 1024; // Denne værdi SKAL ALTID være en effekt på 2 const uint16_t samplingFrequency = 8000; // Vil påvirke timer maks. Værdi i timer_setup () SYSCLOCK/8/samplingFrekvens skal være et heltal
Vi opretter ArduinoFFT -objektet
ArduinoFFT FFT = ArduinoFFT (vReal, vImag, samples, samplingFrequency);
2) Timer og ADC opsætning
Vi indstiller timer 1, så den cykler ved samplingsfrekvensen (8 KHz) og øger en afbrydelse ved output -sammenligning.
ugyldig timer_setup () {
// reset timer 1 TCCR1A = 0; TCCR1B = 0; TCNT1 = 0; TCCR1B = bit (CS11) | bit (WGM12); // CTC, prescaler på 8 TIMSK1 = bit (OCIE1B); OCR1A = ((16000000 /8) / prøveudtagningsfrekvens) -1; }
Og indstil ADC'en, så det
- Bruger A0 som input
- Udløser automatisk på hver timer 1 output sammenlign match B
- Genererer en afbrydelse, når konverteringen er gennemført
ADC -uret er indstillet til 1 MHz ved forskalering af systemuret (16 MHz) med 16. Da hver konvertering tager cirka 13 ure i fuld skala, kan konverteringer opnås med en frekvens på 1/13 = 0,076 MHz = 76 KHz. Samplingsfrekvensen bør være betydeligt lavere end 76 KHz for at lade ADC'en have tid til at prøve dataene. (vi valgte fs = 8 KHz).
ugid adc_setup () {
ADCSRA = bit (ADEN) | bit (ADIE) | bit (ADIF); // slå ADC til, ønsker afbrydelse ved afslutning ADCSRA | = bit (ADPS2); // Prescaler på 16 ADMUX = bit (REFS0) | (adcPin & 7); // indstilling af ADC -input ADCSRB = bit (ADTS0) | bit (ADTS2); // Timer/Counter1 Sammenlign Match B trigger kilde ADCSRA | = bit (ADATE); // Tænd for automatisk udløsning}
Vi erklærer afbrydelsesbehandleren, der vil blive kaldt efter hver ADC -konvertering, til at gemme de konverterede data i vReal -arrayet og rydde afbrydelsen
// ADC komplet ISR
ISR (ADC_vect) {vReal [resultNumber ++] = ADC; hvis (resultNumber == prøver) {ADCSRA = 0; // sluk for ADC}} EMPTY_INTERRUPT (TIMER1_COMPB_vect);
Du kan få en udtømmende forklaring på ADC -konvertering på Arduino (analogRead).
3) Opsætning
I opsætningsfunktionen rydder vi den imaginære datatabel og kalder timeren og ADC -opsætningsfunktionerne
nul (); // en funktion, der satte alle de imaginære data til 0 - forklaret i det foregående afsnit
timer_setup (); adc_setup ();
3) Sløjfe
FFT.dcRemoval (); // Fjern DC -komponenten i dette signal, da ADC'en refereres til jord
FFT.windowing (FFTWindow:: Hamming, FFTDirection:: Forward); // Vej data FFT.compute (FFTDirection:: Frem); // Beregn FFT FFT.complexToMagnitude (); // Beregn størrelser // udskrivning af spektret og grundfrekvensen f0 PrintVector (vReal, (prøver >> 1), SCL_FREQUENCY); float x = FFT.majorPeak (); Serial.print ("f0 ="); Serial.print (x, 6); Serial.println ("Hz");
Vi fjerner DC -komponenten, fordi ADC'en refereres til jord, og signalet er cirka centreret omkring 2,5 volt.
Derefter beregner vi dataene som forklaret i det foregående eksempel.
Trin 8: Analyse af et reelt signal - Resultater

Vi ser faktisk kun en frekvens i dette enkle signal. Den beregnede grundfrekvens er 440,118194 Hz. Her er værdien igen en meget tæt tilnærmelse til den reelle frekvens.
Trin 9: Hvad med et afklippet sinusformet signal?

Lad os nu overdrive lidt ADC'en ved at øge signalets amplitude over 5 volt, så det klippes. Skub ikke for meget for ikke at ødelægge ADC -input!
Vi kan se nogle harmoniske optræden. Klipning af signalet skaber højfrekvente komponenter.
Du har set det grundlæggende i FFT -analyse på et Arduino -bord. Nu kan du prøve at ændre samplingsfrekvensen, antallet af prøver og vinduesparameteren. Biblioteket tilføjer også en parameter til at beregne FFT hurtigere med mindre præcision. Du vil bemærke, at hvis du indstiller samplingsfrekvensen for lav, vil de beregnede størrelser fremstå fuldstændig fejlagtige på grund af spektralfoldning.
Anbefalede:
DIY -- Sådan laver du en edderkoprobot, der kan kontrolleres ved hjælp af smartphone ved hjælp af Arduino Uno: 6 trin

DIY || Sådan laver du en edderkoprobot, der kan styres ved hjælp af smartphone Brug af Arduino Uno: Mens du laver en edderkoprobot, kan man lære så mange ting om robotik. Ligesom at lave robotter er underholdende såvel som udfordrende. I denne video vil vi vise dig, hvordan du laver en Spider -robot, som vi kan betjene ved hjælp af vores smartphone (Androi
Kontrol ledt over hele verden ved hjælp af internet ved hjælp af Arduino: 4 trin

Kontrol ledt over hele verden ved hjælp af internet ved hjælp af Arduino: Hej, jeg er Rithik. Vi kommer til at lave en internetstyret LED ved hjælp af din telefon. Vi kommer til at bruge software som Arduino IDE og Blynk.Det er enkelt, og hvis det lykkedes dig, kan du styre så mange elektroniske komponenter, du ønskerTing We Need: Hardware:
Sådan laver du en drone ved hjælp af Arduino UNO - Lav en quadcopter ved hjælp af mikrokontroller: 8 trin (med billeder)

Sådan laver du en drone ved hjælp af Arduino UNO | Lav en Quadcopter ved hjælp af mikrokontroller: Introduktion Besøg min Youtube -kanal En Drone er en meget dyr gadget (produkt) at købe. I dette indlæg vil jeg diskutere, hvordan jeg gør det billigt ?? Og hvordan kan du lave din egen sådan til en billig pris … Nå i Indien alle materialer (motorer, ESC'er
RF 433MHZ radiostyring ved hjælp af HT12D HT12E - Lav en RF -fjernbetjening ved hjælp af HT12E & HT12D med 433mhz: 5 trin

RF 433MHZ radiostyring ved hjælp af HT12D HT12E | Oprettelse af en RF -fjernbetjening ved hjælp af HT12E & HT12D med 433mhz: I denne instruktør vil jeg vise dig, hvordan du laver en RADIO -fjernbetjening ved hjælp af 433mhz sendermodtagermodul med HT12E -kode & HT12D -dekoder IC.I denne instruktive kan du sende og modtage data ved hjælp af meget meget billige KOMPONENTER SOM: HT
Trådløs fjernbetjening ved hjælp af 2,4 GHz NRF24L01 -modul med Arduino - Nrf24l01 4 -kanals / 6 -kanals sender modtager til Quadcopter - Rc Helikopter - Rc -fly ved hjælp af Arduino: 5 trin (med billeder)
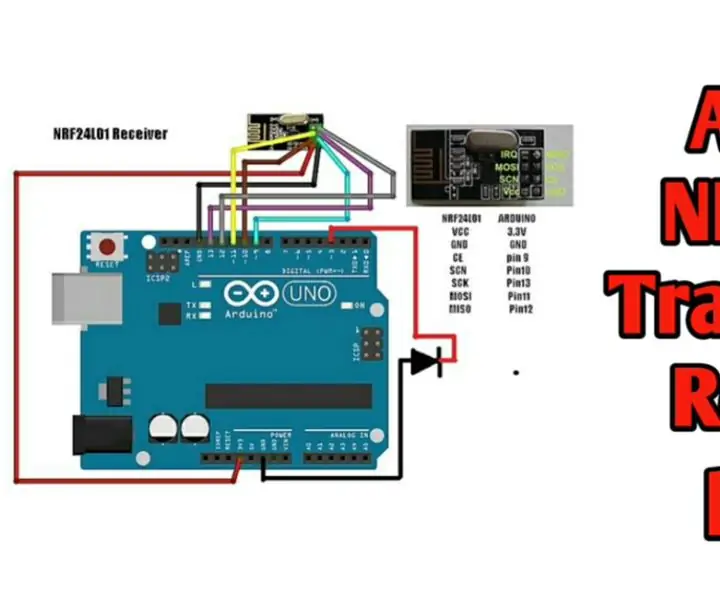
Trådløs fjernbetjening ved hjælp af 2,4 GHz NRF24L01 -modul med Arduino | Nrf24l01 4 -kanals / 6 -kanals sender modtager til Quadcopter | Rc Helikopter | Rc -fly ved hjælp af Arduino: At betjene en Rc -bil | Quadcopter | Drone | RC -fly | RC -båd, vi har altid brug for en modtager og sender, antag at vi til RC QUADCOPTER har brug for en 6 -kanals sender og modtager, og den type TX og RX er for dyr, så vi laver en på vores
