2-knappers kvadratisk ligningsløser: 5 trin

2024 Forfatter: John Day | [email protected]. Sidst ændret: 2024-01-30 08:27

Introduktion

velkommen til min første instruerbare!

Jeg startede dette projekt for at udvide min programmeringskendskab. Ofte fletter du bare forskellige kildekoder for at oprette det program, du har brug for. Mit mål var at skrive min egen programkode til interaktion med et værktøj. Jeg kunne godt lide at lave et simpelt værktøj til beregning. For en måned siden støttede jeg en ven til at løse andengradsligning.

Bazinga! dette er brugssagen!

Jeg genbrugte en gammel metalkasse. Jeg foretrak det minimalistiske udseende og interface af værktøjer. det er grunden til, at jeg bare vil bruge 2 knapper til at give input. Kampen vil blive vist med et simpelt LCD -display.

Forbrugsvarer

materialeliste:

boks

Arcade -stil med 2 knapper

Arduino Nano eller lignende

LCD -display 1602 med I2C -adapter

tænd/sluk -kontakt

ledninger

2x 10k Ohm modstand

batteri 9v blok

stik til 9v batteri

brødbræt

diverse (træstykke, metalvinkel, kabelbindere, skruer, skiver)

værktøjer:

sav

loddekolbe

boremaskine

computer til programmering

Trin 1: Matematisk baggrund

Matematisk baggrund

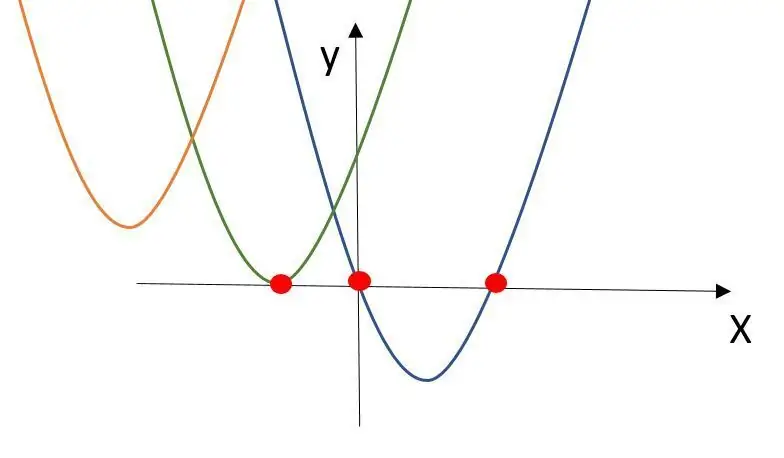
Kvadratisk ligning med 2 knapper viser de værdier, hvor den kvadratiske funktion krydser X-aksen. En kvadratisk funktion kan krydse X-aksen aldrig, en eller to gange.

Der er forskellige måder at beregne disse værdier på. Til mit værktøj bruger jeg PQ-formlen (jeg er ikke sikker på, om dette udtryk vil blive brugt over hele verden).

En kvadratisk ligning har formen:

ax²+bx+c = 0

For at beregne krydsningspunkterne divideres formularen med a x²+px+q = 0 med p = b/a; q = c/a

PQ -formlen:

x1 = -p/2 + sqrt ((p/2) ² -q)

x2 = -p/2 -sqrt ((p/2) ² -q)

Resultatet x kan få 0, 1 eller 2 værdier. Det afhænger af værdien under kvadratroden.

Er værdien> 0, så har PQ-formlen to løsninger.

Er værdien = 0, så har PQ-formlen en løsning

er værdien <0, så har PQ -formlen ingen løsning. Funktionen krydser ikke X-aksen.

Trin 2: Software

Software

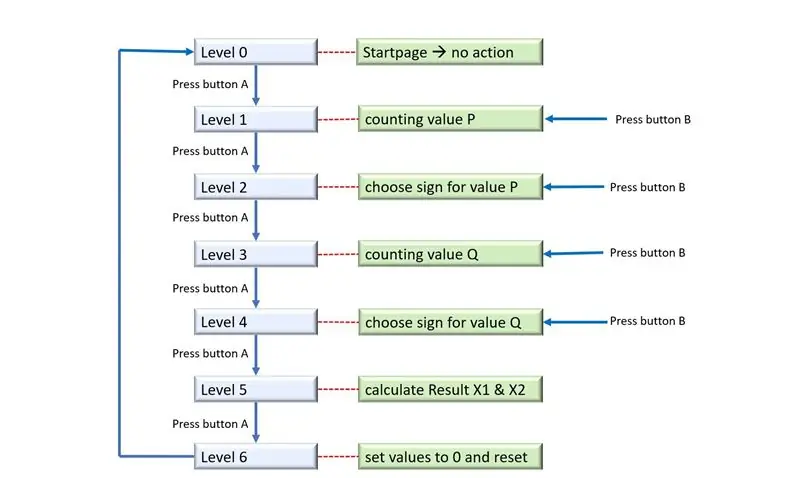
Til programmering brugte jeg den officielle Arduino IDE. Mit mål var at oprette mit eget softwareprogram. Min grænseflade skal have to knapper. En knap til at gå mellem forskellige niveauer, den anden knap til at ændre værdierne i de forskellige niveauer.

For at løse PQ-formlen opretter jeg strukturen ovenfor:

Helt sikkert genopfinder jeg ikke hjulet. Til oprettelse af koden brugte jeg modulet:

- debounce

- Skærm

Følgende punkter var de største udfordringer:

- Hvordan kan jeg vælge skiltet? Jeg løste denne udfordring med funktionen modulo (link). Koden deler input med 2. Er input et ulige tal, værdien bliver negativ, ellers er tallet positivt.

- Efter at have gennemgået alle niveauer, skal jeg erklære alle værdier til 0.

- Den viste tekst sletter bare afsendelsestegnene. Hvis koderne sender et ord med 4 tegn, genindlæses kun disse 4 tegn. Hvis ordet før havde flere tegn, forbliver tegnene. For at løse det vil den viste tekst blive fyldt op med emner. Alle 16 tegn i træk genindlæses.

Den endelige kode er vedhæftet.

Trin 3: Hardware

Hardware

Dele er angivet ovenfor. Til dette projekt er hardwaren enkel. Jeg mangler bare en Arduino mikroprocessor, 2 knapper og et display. Okay, hvis du kan lide at putte i en kasse, har du også brug for en kasse og strømforsyning.

Jeg genbruger en gammel metalkasse. Jeg borede et hul i knappen for at tilslutte kontakten til strømforsyning. Kassedækslet fik 3 huller. Jeg borede to huller til de store knapper og skar et vindue til displayet. Jeg stikker et lille stykke træ bag omslaget for at have flere ting til at reparere display og knapper. For at opgradere udseendet fik æsken klistermærker.

Til strømforsyning anbefaler jeg genopladelige 9V blokbatterier. Jeg tilslutter batteriet via afbryderen til Arduino. Batteriet er fastgjort til kassen med en lille metalvinkel. Stikket til batteriet er bare fastgjort med kabelbindere.

Mikroprocessoren er en klon af en Arduino nano. I dette tilfælde er ydelsen tilstrækkelig. En Attiny 85, for eksempel en Digispark -mikroprocessor, blev afvist. Arduinoen er "brødbrættet" ved siden af displayet.

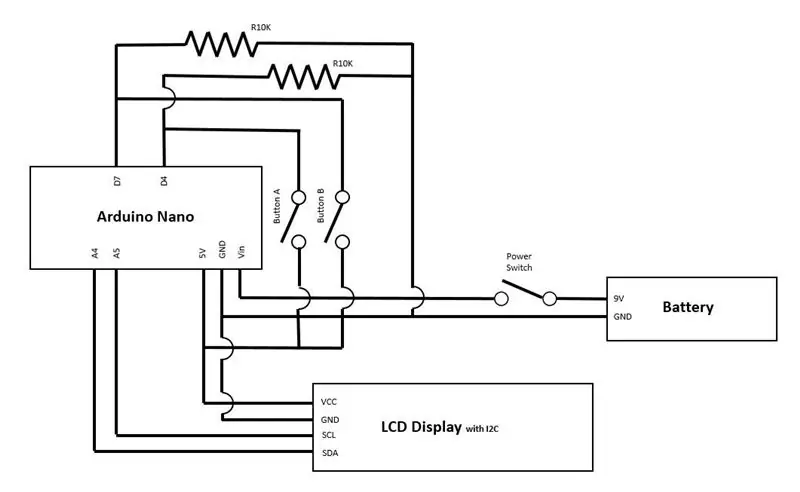
Displayet er et 1602 LCD -display. du kan bruge 16 tegn i to rækker. Du kan finde denne skærm i mange forskellige maskiner og værktøjer. Der er to forskellige måder at bruge dette display på. Du kan slutte skærmen direkte til controlleren, eller du kan bruge et tilføjelsesprogram til at kommunikere med displayet via I2C. I2C er en standardprotokol. Jeg brugte det, fordi det er lettere at slutte skærmen til controlleren. Du skal bare bruge 4 kabler i stedet for 16, VCC til 5V, GND til GND, SDA til A4, SCL til A5. Displayet fastgøres med skruer til boksens dæksel.

Knapperne er enorme! de har den typiske arkadespilstil. Jeg kan lide det! Knapperne er forbundet til digital pin 4 og 7. Glem ikke 10K modstanderne!

For at åbne dækslet, f.eks. For at skifte batteri, brugte jeg længere kabler, der var tilsluttet brødbrættet.

Trin 4: Ledningsføring

Trin 5: Fremtidig forbedring

Fremtidig forbedring

Efter afslutning af et projekt finder du altid fejl eller funktioner til forbedring. I dette projekt er jeg glad for bare at finde et par punkter, jeg ville forbedre for fremtiden.

Til næste gang ville jeg forbedre udnyttelsen i boksen. Jeg fikseret displayet, afbryderen og knapperne i begyndelsen af dette projekt. Til sidst fik jeg lidt problemer med at finde plads nok til batteriet og mikroprocessoren i kassen. Når jeg lagde knappen og displayet mere udenfor, ville jeg ikke have problemer med pladsen til delene inde i boksen.

I øjeblikket har jeg ikke en use case til løsning af kvadratisk ligning. For at forbedre værktøjet vil jeg gerne udvide værktøjet med yderligere matematiske ting, for eksempel grundregning eller formler som binominel formel eller sætning i Pythagoras.