Indholdsfortegnelse:
- Trin 1: Use Case: Udjævning af ADC -målinger
- Trin 2: Brug Case: Måling af DC -komponent i mikrofonsignal
- Trin 3: Beregning
- Trin 4: Koden
- Trin 5: Ekstraudstyr
- Trin 6: Konklusion
Video: Løbende gennemsnit for dine mikrokontrollerprojekter: 6 trin

2024 Forfatter: John Day | [email protected]. Sidst ændret: 2024-01-30 08:26

I denne instruktive vil jeg forklare, hvad et løbende gennemsnit er, og hvorfor du skal bekymre dig om det, samt vise dig, hvordan det skal implementeres for maksimal beregningseffektivitet (bekymre dig ikke om kompleksitet, det er meget enkelt at forstå, og jeg vil giver også et brugervenligt bibliotek til dine arduino -projekter:)
Løbende gennemsnit, også almindeligvis omtalt som glidende gennemsnit, glidende middel eller løbende middel, er et udtryk, der bruges til at beskrive gennemsnitsværdien af sidste N -værdier i dataserier. Det kan beregnes lige som normalt gennemsnit, eller du kan bruge et trick til at få det til at have en minimal indvirkning på din kode.
Trin 1: Use Case: Udjævning af ADC -målinger

Arduino har en anstændig 10 bit ADC med meget lidt støj. Når man måler værdi på en sensor som f.eks. Potentiometer, fotoresistor eller andre støjende komponenter, er det svært at stole på, at målingen er korrekt.
En løsning er at tage flere målinger, hver gang du vil læse din sensor og beregne dem i gennemsnit. I nogle tilfælde er dette en levedygtig løsning, men ikke altid. Hvis du ville læse ADC 1000 gange i sekundet, ville du skulle have 10 000, hvis du i gennemsnit tog 10 målinger. Et enormt spild af beregningstid.
Min foreslåede løsning er at foretage målinger 1000 gange i sekundet, opdatere løbende gennemsnit hver gang og bruge det som aktuel værdi. Denne metode introducerer en vis latenstid, men reducerer beregningskompleksiteten i din applikation, hvilket giver dig meget mere tid til yderligere behandling.
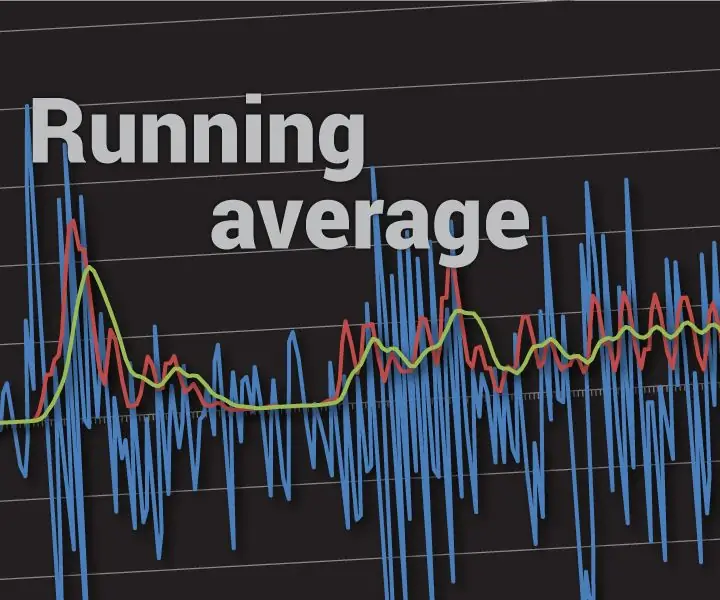
På billedet ovenfor brugte jeg løbende gennemsnit af de sidste 32 målinger. Du vil se, at denne metode ikke er 100% fejlsikker, men det forbedrer nøjagtigheden markant (det er ikke værre end at gennemsnit 32 prøver hver gang). Hvis du ville beregne et gennemsnit på 32 målinger hver gang, ville det tage over 0,25 ms på Arduino UNO til målinger alene!
Trin 2: Brug Case: Måling af DC -komponent i mikrofonsignal



Arduino kan måle spændinger mellem 0 og Vcc (normalt 5 V). Lydsignal er fuldstændig AC, og hvis du vil måle det på en mikrokontroller, skal du forspænde det omkring 1/2 Vcc. I et Arduino UNO -projekt ville det betyde cirka 2,5 V (DC) + lydsignal (AC). Ved brug af 10 bit ADC og 5 V strømforsyning skal 2,5 V bias være lig med måling på 512. Så for at få en AC -værdi for signalet, skal 512 trækkes fra ADC -måling, og det er det, ikke?
I en ideel verden ville det være sandt. Desværre er det virkelige liv mere kompliceret, og vores signalforstyrrelser har en tendens til at glide. Meget almindelig er 50 Hz støj (60 Hz, hvis du bor i USA) fra det elektriske netværk. Normalt er det ikke alt for problematisk, men det er godt at vide, at det findes. Mere problematisk er lineær drift fra opvarmning af komponenter. Du indstiller omhyggeligt DC -offset -korrektion ved start, og den driver langsomt væk, mens din applikation kører.
Jeg vil illustrere dette problem med en (musik) beat -detektor. Du konfigurerer din bias -fjernelse, og beats er klare (billede 2). Efter et stykke tid bevæger DC -bias sig, og beats er næppe mærkbare for mikrokontrolleren (billede 3). Slagdetekteringsalgoritme vil blive undersøgt i dybden i en fremtidig instruktion, da den overstiger omfanget af denne artikel.
Heldigvis er der en måde at konstant beregne lydens DC -offset. Det vil ikke komme som en overraskelse, at løbende gennemsnit, emnet for dette instruerbare, giver en løsning.
Vi ved, at gennemsnitsværdien for ethvert vekselstrømsignal er 0. Ved hjælp af denne viden kan vi trække den gennemsnitlige værdi af vekselstrøm+jævnstrømsignal, er dens jævnstrømsspænding. For at fjerne det kan vi tage et løbende gennemsnit af de sidste par værdier og trække det fra den aktuelle ADC -læsning. Bemærk, at du skal bruge et lang nok løbende gennemsnit. For lyd bør en tiendedel af et sekund (antallet af prøver afhænger af din samplingsrate) være tilstrækkeligt, men ved, at længere gennemsnit fungerer bedre. På det første billede kan du se et eksempel på reel DC -bias -beregning med løbende gennemsnit med 64 elementer ved 1 kHz samplingshastighed (mindre end jeg anbefalede, men det virker stadig).
Trin 3: Beregning

Du kan forestille dig løbende gennemsnit som en gennemsnitlig vægt af mennesker i lægens venteværelse. Læge afslutter undersøgelsen af en patient og samtidig går en ny ind i venteværelset.
For at finde ud af gennemsnitsvægten for alle ventende patienter i venteværelset, kunne sygeplejersken derefter spørge hver patient om deres vægt, tilføje disse tal og dividere med antallet af patienter. Hver gang lægen tager imod en ny patient, gentager sygeplejersken hele processen.
Du tænker måske: "Det lyder ikke alt for effektivt … Der må være en bedre måde at gøre dette på." Og du ville have ret.
For at optimere denne proces kunne sygeplejersken føre en oversigt over den samlede vægt af den nuværende patientgruppe. Når lægen kalder ny patient ind, ville sygeplejersken spørge ham om hans vægt og trække den fra gruppens total og lade ham gå. Sygeplejerske ville derefter spørge patienten, der lige gik ind i venteværelset om sin vægt og tilføje den til totalen. Gennemsnitlig vægt af patienter efter hvert skift ville være summen af vægte divideret med antal patienter (ja, det samme som før, men nu spurgte sygeplejerske kun to personer om deres vægt i stedet for dem alle). Jeg er klar over, at dette afsnit måske var lidt forvirrende, så se illustrationen ovenfor for yderligere klarhed (eller stil spørgsmål i kommentarer).
Men selvom du ikke synes, at det sidste afsnit var forvirrende, kan du have spørgsmål som f.eks. Hvad der skulle være i akkumulatoren i begyndelsen, hvordan skal jeg lægge det, jeg lige læste, i en egentlig C -kode? Det vil blive behandlet i næste trin, hvor du også får min kildekode.
Trin 4: Koden

For at beregne løbende gennemsnit skal du først gemme de sidste N -værdier. du kunne have en matrix med N -elementer og flytte hele indholdet ét sted hver gang du tilføjer et element (gør venligst ikke dette), eller du kan overskrive et gammelt element og justere markøren til det næste element, der skal smides ud (gør venligst dette:)
Akkumulator skal starte initialiseret til 0, det samme gælder for alle elementer i forsinkelseslinje. I andre tilfælde vil dit løbende gennemsnit altid være forkert. Du vil se, at delayLine_init sørger for at initialisere forsinkelseslinjen, du skal selv sørge for akkumulator.
tilføjelse af et element til forsinkelseslinje er lige så let som at reducere indekset for det nyeste element med 1, og sørg for at det ikke peger på siden af forsinkelseslinjearrayet. efter faldende indeks, når det er 0, vil det gå rundt til 255 (fordi det er et 8 -bit usigneret heltal). Modulo (%) -operatør med størrelsen på forsinkelseslinjearray vil sikre, at indeks peger på et gyldigt element.
Beregning af et løbende gennemsnit burde være let at forstå, hvis du fulgte min analogi i forrige trin. Træk ældste element fra akkumulator, tilføj nyeste værdi til akkumulator, skub nyeste værdi til forsinkelseslinjen, returner akkumulator divideret med antal elementer.
Let, ikke?
Du er velkommen til at eksperimentere med at bruge den vedhæftede kode for bedre at forstå, hvordan alt dette fungerer. Som det er i øjeblikket, læser arduino analog værdi på analog pin A0 og udskriver "[ADC værdi], [løbende gennemsnit]" på seriel port ved 115200 baud rate. Hvis du åbner arduinos serielle plotter med korrekt baudhastighed, vil du se to linjer: ADC -værdi (blå) og udjævnet værdi (rød).
Trin 5: Ekstraudstyr

Der er et par ting, du ikke nødvendigvis behøver at vide for at bruge løbende gennemsnit i dit projekt, det vil ikke skade at vide.
forsinkelse: Jeg vil starte med at tale om illustration af dette trin. Du vil bemærke, at løbende gennemsnit af flere elementer medfører større forsinkelse. Hvis din svartid for at ændre værdi er kritisk, kan du bruge et kortere løbende gennemsnit eller øge samplingshastigheden (mål oftere).
Komme videre.
initialisering: Da jeg talte om at initialisere akkumulator og forsinkelseselementer, sagde jeg, at du skulle initialisere dem alle til 0. Alternativt kan du initialisere forsinkelseslinje til alt, hvad du kan lide, men akkumulatoren skal starte som en sum af de nyeste N -elementer i forsinkelseslinjen (hvor N er antallet af elementer i dit løbende gennemsnit). Hvis akkumulator starter som en hvilken som helst anden værdi, vil det beregnede gennemsnit være forkert - enten for lavt eller for højt, altid med det samme beløb (under forudsætning af de samme indledende betingelser). Jeg foreslår, at du prøver at lære hvorfor det er sådan ved at bruge en "pen og papirsimulering".
akkumulatorstørrelse: Du skal også bemærke, at akkumulatoren skal være stor nok til at gemme summen af alle elementer i forsinkelseslinjen, hvis de alle er positive eller negative max. Det betyder praktisk talt, at akkumulator skal være en datatype større end forsinkelseslinjeelementer og signeret, hvis forsinkelseslinjeelementer er signeret.
trick: Lange forsinkelseslinjer fylder meget i hukommelsen. Det kan hurtigt blive et problem. Hvis du er meget hukommelsesbegrænset og ikke bekymrer dig meget om nøjagtighed, kan du tilnærme løbende gennemsnit ved helt at udelade forsinkelse og gøre dette i stedet: trække 1/N * akkumulator fra akkumulator og tilføje ny værdi (på eksempel på 8 lange løbende gennemsnit: akkumulator = akkumulator * 7/8 + nyVærdi). Denne metode giver et forkert resultat, men det er en anstændig metode til at beregne løbende gennemsnit, når du mangler hukommelse.
lingvistik: "løbende gennemsnit/middel" bruges typisk, når der henvises til gennemsnit i realtid, mens "glidende gennemsnit/middelværdi" normalt betyder, at algoritmen kører på statiske datasæt, f.eks. Excel -regneark.
Trin 6: Konklusion
Jeg håber, at denne instruktive var let nok at forstå, og at den vil hjælpe dig i dine fremtidige projekter. Du er velkommen til at stille spørgsmål i kommentarerne herunder, hvis der er noget uklart.
Anbefalede:
Tilslut og eftermonter dine tilsluttede løsninger med Hologram Nova og Ubidots: 9 trin

Tilslut og eftermonter dine tilsluttede løsninger med Hologram Nova og Ubidots: Brug din Hologram Nova til at eftermontere infrastruktur. Konfigurer Hologram Nova ved hjælp af en Raspberry Pi til at sende (temperatur) data til Ubidots. I den følgende vejledning vil Ubidots demonstrere, hvordan du konfigurerer et Hologram Nova ved hjælp af en Raspberry Pi og viser en te
Lav nemt dine egne widgets - Hurtig BPM -tæller: 6 trin
Lav nemt dine egne widgets - Hurtig BPM -tæller: Webapps er almindeligt, men webapps, der ikke kræver internetadgang, gør det ikke. I denne artikel viser jeg dig, hvordan jeg lavede en BPM -tæller på en simpel HTML -side kombineret med vanilje javascript ( se her). Hvis downloadet, kan denne widget bruges offline
ArduBand - Gem dine øjne !: 6 trin (med billeder)

ArduBand - Save Your Eyes !: Hej, i den nuværende situation arbejder mange mennesker derhjemme, og derfor bruger vi meget mere tid foran computere eller smartphones. Nogle gange kan vi sidde foran skærmen i flere timer, ødelægge vores øjne og krumme ryggen. Vi kunne bruge en
CP2 Excel -vægtet gennemsnit: 14 trin
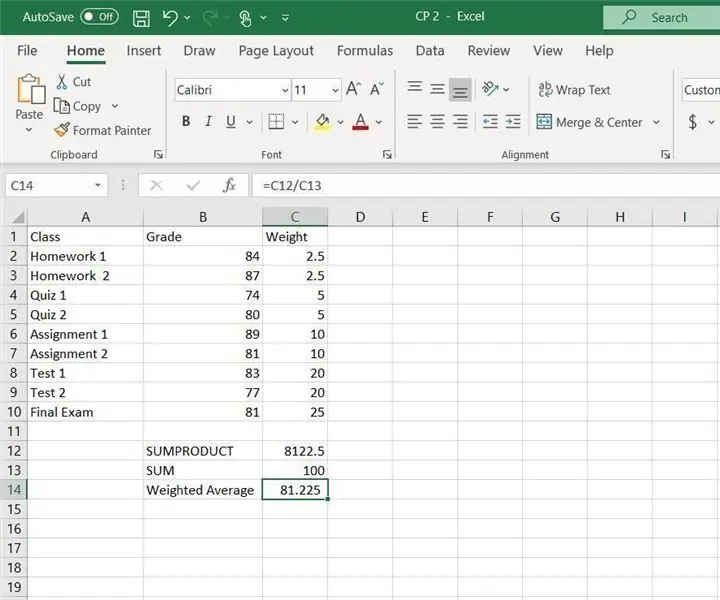
CP2 Excel Vægtet Gennemsnit: Instruktioner til beregning af det vejede gennemsnit i Excel. I dette eksempel bruges funktionen SUMPRODUCT og SUM i Excel. Det vejede gennemsnit er nyttigt til at beregne den samlede karakter for en klasse
Løbende LED -lufthavnsbane: 7 trin

Running LED Airport Runway: Dette er en revision og inspiration fra https://www.instructables.com/id/Running-LEDs-Ardu…Jeg ændrer kildekoden for at få lyset til at blinke frem og tilbage og langsommere.Dette er en håndlavet model af Airport Runway
